ГДЗ по Математике 5 Класс Часть 1 Номер 47 Мнемозина Виленкин, Жохов — Подробные Ответы

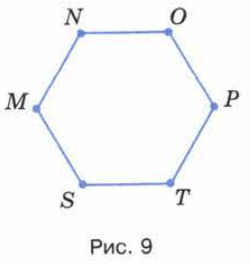
Назовите вершины и стороны шестиугольника на рисунке 9.

Вершинами шестиугольника являются точки М, N, О, Р, Т, S.
Сторонами шестиугольника являются отрезки MN, NO, OP, PT, TS, SM.

Вершины шестиугольника обозначены точками $M$, $N$, $O$, $P$, $T$ и $S$, а его стороны — отрезками $MN$, $NO$, $OP$, $PT$, $TS$ и $SM$. Рассмотрим этот шестиугольник в более детализированном контексте.

Для начала, шестиугольник — это многоугольник, состоящий из шести сторон, каждая из которых соединяет две соседние вершины. Вершины и стороны шестиугольника представляют собой замкнутую фигуру, где каждая вершина соединена с двумя другими вершинами.

Структура шестиугольника

Вершины шестиугольника:

$M$, $N$, $O$, $P$, $T$, $S$ — шесть точек, которые служат вершинами многоугольника. Эти вершины соединены сторонами, образующими углы между соседними отрезками.

Стороны шестиугольника:

$MN$ — отрезок, соединяющий вершины $M$ и $N$.

$NO$ — отрезок, соединяющий вершины $N$ и $O$.

$OP$ — отрезок, соединяющий вершины $O$ и $P$.

$PT$ — отрезок, соединяющий вершины $P$ и $T$.

$TS$ — отрезок, соединяющий вершины $T$ и $S$.

$SM$ — отрезок, соединяющий вершины $S$ и $M$, замыкающий шестиугольник.

Применение геометрических свойств

1. Внутренние углы шестиугольника:
   Внутренние углы многоугольника можно вычислить по формуле для суммы углов многоугольника:

   $$\text{Сумма внутренних углов шестиугольника} = (n — 2) \times 180^\circ,$$

   где $n = 6$ — количество сторон. Подставляем:

   $$\text{Сумма внутренних углов} = (6 — 2) \times 180^\circ = 720^\circ.$$

   Это означает, что сумма внутренних углов шестиугольника равна 720 градусам.

2. Равносторонний шестиугольник:
   Если шестиугольник является равносторонним, то все его стороны равны между собой, и все углы равны. В этом случае каждый внутренний угол будет:

   $$\text{Внутренний угол} = \frac{720^\circ}{6} = 120^\circ.$$

3. Равнобедренный шестиугольник:
   В равнобедренном шестиугольнике стороны, не являющиеся противоположными, могут быть равными, но углы между ними будут варьироваться в зависимости от формы.
4. Диагонали шестиугольника:
   Диагонали шестиугольника — это отрезки, соединяющие не соседние вершины. В случае выпуклого шестиугольника существует несколько типов диагоналей, которые могут быть как длинными, так и короткими в зависимости от конфигурации.

Заключение

Таким образом, шестиугольник с вершинами $M$, $N$, $O$, $P$, $T$, $S$ и сторонами $MN$, $NO$, $OP$, $PT$, $TS$, $SM$ имеет следующие ключевые характеристики:

• Внутренние углы в сумме дают 720°.
• В равностороннем шестиугольнике каждый угол составляет 120°.
• Если шестиугольник не равносторонний, то углы и длины сторон могут варьироваться в зависимости от его конфигурации.