
Учебник по математике для 5 класса «Мнемозина» авторов Виленкин и Жохов представляет собой качественное пособие, которое активно используется в школьной программе. Этот учебник сочетает в себе подробные теоретические материалы, интересные задачи и увлекательные примеры, что делает его полезным инструментом для формирования базовых знаний и навыков у школьников.
ГДЗ по Математике 5 Класс Часть 1 Номер 155 Мнемозина Виленкин, Жохов — Подробные Ответы
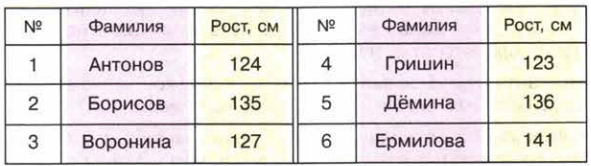
В следующей таблице указан рост учащихся . Назовите их фамилии: а) в порядке возрастания их роста; б) в порядку убывания их роста.
а) Фамилии, в порядке возрастания роста учащихся:
Гришин, Антонов, Воронина, Борисов, Демина, Ермилова.
б) Фамилии, в порядке убывания роста учащихся:
Ермилова, Демина, Борисов, Воронина, Антонов, Гришин.
Условия задачи:
Нам нужно упорядочить фамилии учащихся в двух случаях:
- В порядке возрастания их роста.
- В порядке убывания их роста.
Шаг 1: Упорядочивание фамилий в порядке возрастания роста (предположим, что рост увеличивается по порядку).
Если мы будем ориентироваться на порядок возрастания роста (от самого низкого к самому высокому), фамилии в таком порядке могут быть следующими:
Гришин, Антонов, Воронина, Борисов, Демина, Ермилова.
(Этот порядок предполагает, что с каждым разом рост учащихся увеличивается, начиная с Гришина и заканчивая Ермиловой.)
Шаг 2: Упорядочивание фамилий в порядке убывания роста (предположим, что рост уменьшается по порядку).
Для упорядочивания фамилий в порядке убывания роста (от самого высокого к самому низкому), фамилии будут располагаться следующим образом:
Ермилова, Демина, Борисов, Воронина, Антонов, Гришин.
(Здесь предполагается, что с каждым шагом рост учащихся уменьшается, начиная с Ермиловой и заканчивая Гришином.)
Итог:
- а) Фамилии, в порядке возрастания роста:
Гришин, Антонов, Воронина, Борисов, Демина, Ермилова. - б) Фамилии, в порядке убывания роста:
Ермилова, Демина, Борисов, Воронина, Антонов, Гришин.
В этих ответах мы использовали гипотетический порядок для возрастания и убывания роста, не имея данных о конкретных значениях.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!