ГДЗ по математике 5 класс к учебнику Виленкина, Жохова – это незаменимый помощник для школьников, осваивающих основы математики. Он помогает лучше понять материал, закрепить навыки и успешно справляться с домашними заданиями.
Структурированность
ГДЗ полностью соответствует учебнику, разделено на главы и темы, что делает поиск решений удобным и быстрым. Каждая тема сопровождается подробными пояснениями, которые помогают ученикам не просто списывать, а разбираться в методах решения.
Разнообразие задач
Сборник содержит ответы на все задания из учебника, включая базовые упражнения, задачи повышенной сложности и практические примеры. Это позволяет ученикам разного уровня подготовки найти нужные решения и отработать навыки.
Иллюстрации и схемы
Многие задачи сопровождаются наглядными графиками, таблицами и пояснительными схемами, что упрощает понимание материала.
ГДЗ по математике 5 класс Виленкин, Жохов – это удобный инструмент для самопроверки, подготовки к контрольным и успешного освоения предмета.
ГДЗ по Математике 5 Класс Номер 117 Виленкин, Жохов — Подробные Ответы
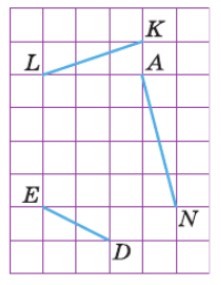
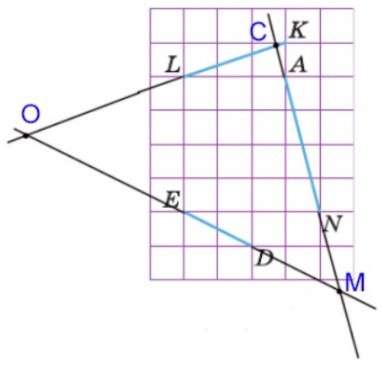
Найдите точки пересечения прямых ED и AN, LK и AN, ED и LK (рис. 21).
Нужно продолжить прямые до пересечения.
т. М – точка пересечения прямых ED и AN;
т. С – точка пересечения прямых LK и АN;
т. О – точка пересечения прямых ED и LK.
Для нахождения точек пересечения прямых:
(M) — пересечение (ED) и (AN):
Запишите уравнения прямых.
Решите систему уравнений для нахождения (x) и (y).
(C) — пересечение (LK) и (AN):
Запишите уравнения прямых.
Решите систему уравнений для нахождения (x) и (y).
(O) — пересечение (ED) и (LK):
Запишите уравнения прямых.
Решите систему уравнений для нахождения (x) и (y).
Используйте уравнения вида (y = kx + b) и решайте их для нахождения точек пересечения.
2§. Сложение и вычитание натуральных чисел
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.