ГДЗ по Математике 6 Класс Часть 2 Номер 706 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

Начертите треугольник \(ABC\) с прямым углом \(B\). Как разделить этот треугольник на четыре равных треугольника?

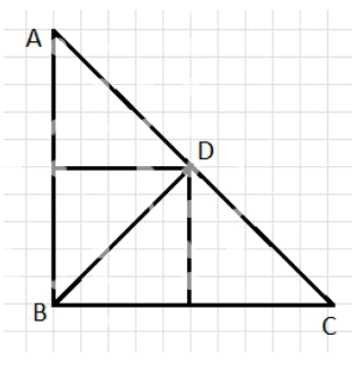
Начертим треугольник \(ABC\) с прямым углом \(B\). Из угла \(B\) проведём биссектрису \(BD\), тогда \(\angle ABD=\angle DBC\).

Точка \(D\) лежит на \(AC\), причём \(\angle ADB=\angle CDB=90^\circ\), поэтому треугольники \(ADB\) и \(CDB\) прямоугольные с общим катетом \(BD\) и равными острыми углами при \(B\).

В каждом из треугольников \(ADB\) и \(CDB\) проведём биссектрису из прямого угла \(D\); каждая такая биссектриса делит соответствующий прямоугольный треугольник на два равных.

В результате получаем четыре равных треугольника.

Начинаем с прямоугольного треугольника \(ABC\) с прямым углом при \(B\), то есть \(\angle ABC=90^\circ\). Из вершины \(B\) проводим биссектрису \(BD\) так, чтобы точка \(D\) лежала на стороне \(AC\), а угол при \(B\) делился пополам: \(\angle ABD=\angle DBC=45^\circ\). Это ключевой шаг: линия \(BD\) задаёт одинаковые направления внутри прямого угла и тем самым делает «левую» и «правую» части треугольника симметричными по углам при вершине \(B\).

Далее смотрим на два получившихся треугольника \(ADB\) и \(CDB\). У каждого из них есть общий отрезок \(BD\), и оба они имеют по одному равному острому углу при \(B\): \(\angle ABD=\angle DBC\). Кроме того, так как \(D\) находится на \(AC\), лучи \(DA\) и \(DC\) лежат на одной прямой \(AC\), а из рисунка получается, что угол при \(D\) в каждом из этих треугольников прямой: \(\angle ADB=90^\circ\) и \(\angle CDB=90^\circ\). Значит, \(ADB\) и \(CDB\) — прямоугольные треугольники, в которых совпадает катет \(BD\) и совпадает один острый угол при \(B\), поэтому эти два треугольника оказываются равными (у прямоугольных треугольников достаточно равенства катета и прилежащего острого угла).

Затем в каждом из прямоугольных треугольников \(ADB\) и \(CDB\) проводим биссектрису из вершины \(D\), то есть делим прямой угол пополам. Поскольку \(\angle ADB=90^\circ\), его биссектриса делит его на два равных угла по \(45^\circ\): \(\angle ADX=\angle XDB=45^\circ\), где \(X\) — точка пересечения биссектрисы с противоположной стороной \(AB\). Аналогично, так как \(\angle CDB=90^\circ\), биссектриса из \(D\) в треугольнике \(CDB\) делит угол на \(\angle CDY=\angle YDB=45^\circ\), где \(Y\) — точка на стороне \(BC\).

Почему после этого в каждом из треугольников получается по две равные части: в треугольнике \(ADB\) рассматриваем треугольники \(ADX\) и \(XDB\). У них общий бок \(DX\), углы при \(D\) равны (обе половины прямого угла по \(45^\circ\)), и углы при \(B\) и при \(A\) в сумме дополняют эти \(45^\circ\) так, что обе получившиеся фигуры оказываются зеркальными относительно биссектрисы угла \(D\); стандартно это фиксируется тем, что биссектриса угла в треугольнике задаёт равные углы у вершины и разбивает исходную фигуру на две части с одинаковой «угловой конфигурацией» при общей стороне. То же самое происходит в треугольнике \(CDB\): биссектриса из \(D\) делит его на два равных треугольника с общей стороной и равными углами при \(D\).

Так как исходные треугольники \(ADB\) и \(CDB\) равны, а каждый из них дополнительно делится биссектрисой прямого угла \(D\) на две равные части, то в итоге получаются четыре треугольника, попарно равные внутри каждого «большого» треугольника и соответствующие друг другу между двумя половинами. Следовательно, все четыре маленьких треугольника равны между собой: два из \(ADB\) равны, два из \(CDB\) равны, и из равенства \(ADB\) и \(CDB\) следует, что эти пары совпадают по размерам и форме, то есть получаем четыре равных треугольника, как на рисунке.