ГДЗ по Математике 6 Класс Часть 2 Номер 684 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

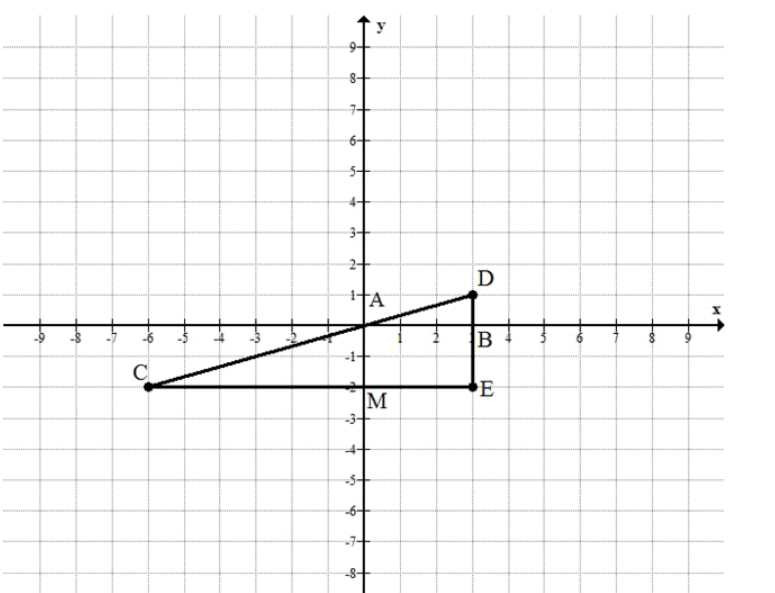
Постройте на координатной плоскости треугольник \(CDE\), если \(C(-6;-2)\), \(D(3;1)\) и \(E(3;-2)\). Запишите координаты точек пересечения сторон треугольника с осями координат.

Сторона \(DE\): \(x=3\), пересечение с осью \(Ox\) при \(y=0\): \(B(3;0)\).

Сторона \(CE\): \(y=-2\), пересечение с осью \(Oy\) при \(x=0\): \(M(0;-2)\).

Сторона \(CD\): \(k=\frac{1-(-2)}{3-(-6)}=\frac{3}{9}=\frac{1}{3}\), уравнение \(y+2=\frac{1}{3}(x+6)\Rightarrow y=\frac{x}{3}\); при \(y=0\) и при \(x=0\) получаем \(A(0;0)\).

Точки пересечения сторон треугольника с осями: \(A(0;0)\), \(B(3;0)\), \(M(0;-2)\).

а) Строим треугольник по заданным координатам: отмечаем точки \(C(-6;-2)\), \(D(3;1)\), \(E(3;-2)\) на координатной плоскости и соединяем их отрезками \(CD\), \(DE\), \(EC\). Точка \(C\) лежит в III четверти, потому что \(x<0\) и \(y<0\); точка \(D\) в I четверти (\(x>0\), \(y>0\)); точка \(E\) в IV четверти (\(x>0\), \(y<0\)).

Далее ищем точки пересечения сторон треугольника с осями \(Ox\) и \(Oy\). Пересечение с осью \(Ox\) означает \(y=0\), а пересечение с осью \(Oy\) означает \(x=0\). Рассматриваем каждую сторону отдельно и находим, выполняется ли на ней условие \(y=0\) или \(x=0\).

б) Сторона \(DE\) соединяет точки \(D(3;1)\) и \(E(3;-2)\). У обеих точек одинаковая абсцисса \(x=3\), значит отрезок \(DE\) — вертикальный и задается уравнением \(x=3\).

Чтобы найти пересечение стороны \(DE\) с осью \(Ox\), используем условие \(y=0\): на оси \(Ox\) координаты имеют вид \((x;0)\). Подставляем в уравнение стороны \(x=3\) и получаем точку \(B(3;0)\). С осью \(Oy\) эта сторона не пересекается, так как для оси \(Oy\) нужно \(x=0\), а на \(DE\) всегда \(x=3\).

в) Сторона \(CE\) соединяет точки \(C(-6;-2)\) и \(E(3;-2)\). У обеих точек одинаковая ордината \(y=-2\), значит отрезок \(CE\) — горизонтальный и задается уравнением \(y=-2\).

Пересечение стороны \(CE\) с осью \(Oy\) находим по условию \(x=0\): на оси \(Oy\) координаты имеют вид \((0;y)\). Подставляем \(x=0\) в уравнение стороны \(y=-2\) и получаем точку \(M(0;-2)\). С осью \(Ox\) эта сторона не пересекается, потому что на оси \(Ox\) требуется \(y=0\), а на \(CE\) всегда \(y=-2\).

г) Сторона \(CD\) соединяет точки \(C(-6;-2)\) и \(D(3;1)\). Чтобы найти ее пересечения с осями, удобно записать уравнение прямой, проходящей через эти две точки. Сначала находим угловой коэффициент: \(k=\frac{1-(-2)}{3-(-6)}=\frac{3}{9}=\frac{1}{3}\).

Далее используем формулу через точку и наклон: \(y-(-2)=\frac{1}{3}(x-(-6))\), то есть \(y+2=\frac{1}{3}(x+6)\). Приводим к более простому виду: \(y+2=\frac{x}{3}+2\), значит \(y=\frac{x}{3}\). Теперь пересечение с осью \(Ox\) ищем из \(y=0\): получаем \(0=\frac{x}{3}\), откуда \(x=0\), значит точка \(A(0;0)\). Пересечение с осью \(Oy\) ищем из \(x=0\): тогда \(y=\frac{0}{3}=0\), снова получаем \(A(0;0)\).

д) Итак, по найденным условиям пересечения сторон треугольника с осями координат получаем три точки: \(B(3;0)\) — это пересечение стороны \(DE\) с осью \(Ox\); \(M(0;-2)\) — это пересечение стороны \(CE\) с осью \(Oy\); \(A(0;0)\) — это точка, в которой сторона \(CD\) пересекает обе оси (она лежит в начале координат).

Проверка согласованности с рисунком: у \(DE\) действительно должна быть вертикаль при \(x=3\), поэтому на оси \(Ox\) получается \(B(3;0)\); у \(CE\) горизонталь при \(y=-2\), поэтому на оси \(Oy\) получается \(M(0;-2)\); а наклонная \(CD\) проходит через начало координат, так как ее уравнение \(y=\frac{x}{3}\) дает \(y=0\) при \(x=0\), значит \(A(0;0)\) соответствует пересечению с осями.