ГДЗ по Математике 6 Класс Часть 2 Номер 683 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

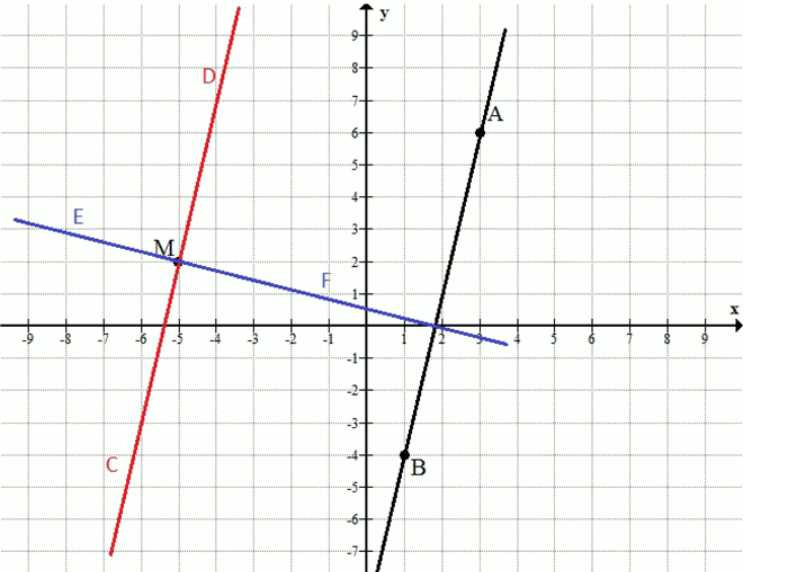
Отметьте на координатной плоскости точки \(A(3;6)\), \(B(1;-4)\) и \(M(-5;2)\). Проведите через точку \(M\) прямую \(CD\), параллельную прямой \(AB\), и прямую \(EF\), перпендикулярную прямой \(AB\).

Найдём угловой коэффициент прямой \(AB\): \(k_{AB}=\frac{6-(-4)}{3-1}=\frac{10}{2}=5\).

Прямая \(CD\) параллельна \(AB\), значит \(k_{CD}=5\) и проходит через \(M(-5;2)\): \(y-2=5(x+5)\), откуда \(y=5x+27\).

Прямая \(EF\) перпендикулярна \(AB\), значит \(k_{EF}=-\frac{1}{5}\) и проходит через \(M(-5;2)\): \(y-2=-\frac{1}{5}(x+5)\), откуда \(y=-\frac{1}{5}x+1\).

а) Для прямой \(AB\) сначала находим её угловой коэффициент, потому что параллельность и перпендикулярность удобнее всего задаются через наклоны прямых. Берём координаты точек \(A(3;6)\) и \(B(1;-4)\) и используем формулу \(k=\frac{y_A-y_B}{x_A-x_B}\).

Подставляем значения: \(k_{AB}=\frac{6-(-4)}{3-1}=\frac{10}{2}=5\). Это означает, что при увеличении \(x\) на \(1\) значение \(y\) на прямой \(AB\) увеличивается на \(5\), то есть прямая \(AB\) имеет достаточно крутой положительный наклон, как на рисунке.

б) Прямая \(CD\) должна проходить через точку \(M(-5;2)\) и быть параллельной \(AB\). Параллельные прямые имеют одинаковый угловой коэффициент, поэтому для \(CD\) берём \(k_{CD}=k_{AB}=5\).

Запишем уравнение через точку и угловой коэффициент: \(y-y_M=k(x-x_M)\). Подставляем \(M(-5;2)\) и \(k=5\): \(y-2=5(x-(-5))=5(x+5)\). Раскрываем скобки: \(y-2=5x+25\), переносим \(-2\) вправо и получаем \(y=5x+27\). Это и есть искомая прямая \(CD\), проходящая через \(M\) и параллельная \(AB\).

в) Прямая \(EF\) должна проходить через ту же точку \(M(-5;2)\), но быть перпендикулярной \(AB\). Для непараллельных прямых в координатной геометрии перпендикулярность выражается так: если \(k_{AB}=5\), то угловой коэффициент перпендикулярной прямой равен отрицательному обратному числу, то есть \(k_{EF}=-\frac{1}{5}\).

Снова используем формулу через точку: \(y-2=-\frac{1}{5}(x+5)\). Чтобы получить вид \(y=kx+b\), раскрываем: \(y-2=-\frac{1}{5}x-\frac{1}{5}\cdot 5=-\frac{1}{5}x-1\). Прибавляем \(2\) к обеим частям: \(y=-\frac{1}{5}x+1\). Это уравнение прямой \(EF\), которая проходит через \(M\) и пересекает прямую \(AB\) под прямым углом, как требуется по условию.