ГДЗ по Математике 6 Класс Часть 2 Номер 682 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

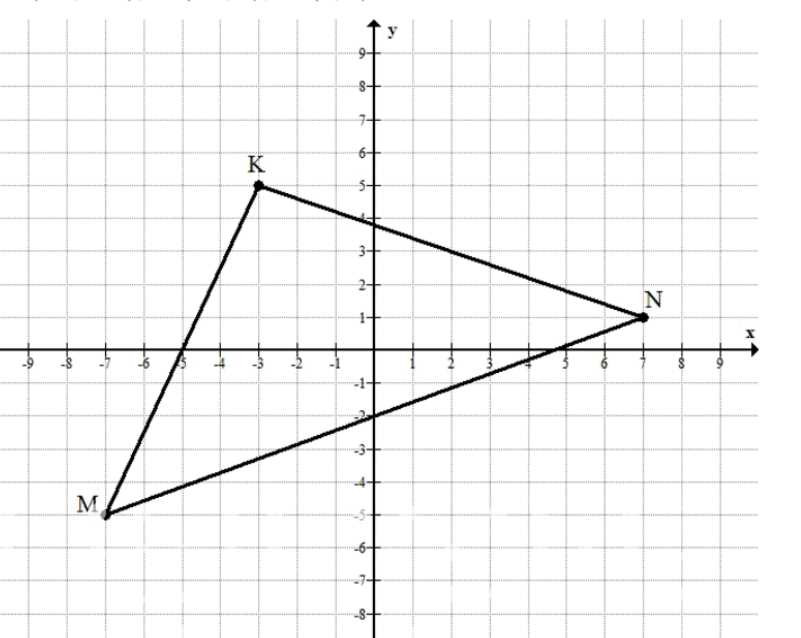
Постройте в координатной плоскости треугольник \(MKN\), если \(M(-7;-5)\), \(N(-3;5)\), \(K(7;1)\). Измерьте углы и стороны этого треугольника. Найдите координаты середины стороны \(MN\).

Точки: \(M(-7;-5)\), \(K(-3;5)\), \(N(7;1)\). Соединяем \(M\), \(K\), \(N\) — получаем треугольник \(MKN\).

Длины сторон (по формуле расстояния \(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)): \(MK=\sqrt{( -3+7)^2+(5+5)^2}=\sqrt{16+100}=\sqrt{116}\approx 5{,}4\) см, \(KN=\sqrt{(7+3)^2+(1-5)^2}=\sqrt{100+16}=\sqrt{116}\approx 5{,}4\) см, \(MN=\sqrt{(7+7)^2+(1+5)^2}=\sqrt{196+36}=\sqrt{232}\approx 7{,}6\) см.

Углы: так как \(MK=KN\), треугольник равнобедренный, а по измерению на чертеже \(\angle K=90^\circ\), тогда \(\angle M=\angle N=45^\circ\).

Середина стороны \(MN\): \(x_0=\frac{x_M+x_N}{2}=\frac{-7+7}{2}=0\), \(y_0=\frac{y_M+y_N}{2}=\frac{-5+1}{2}=-2\), значит середина \(MN\) имеет координаты \((0;-2)\).

а) На координатной плоскости отмечаем точку \(M(-7;-5)\): от начала координат идём на \(7\) единиц влево (по оси \(x\)) и на \(5\) единиц вниз (по оси \(y\)). Аналогично отмечаем точку \(K(-3;5)\): \(3\) единицы влево и \(5\) единиц вверх. Затем отмечаем точку \(N(7;1)\): \(7\) единиц вправо и \(1\) единицу вверх.

После того как три точки нанесены, соединяем их отрезками \(MK\), \(KN\) и \(MN\). Получается треугольник \(MKN\); его стороны — это отрезки, соединяющие пары вершин, а углы расположены в точках \(M\), \(K\), \(N\). Именно в таком порядке и строится треугольник по заданным координатам.

б) Чтобы измерить стороны по координатам (и понять, почему на рисунке получаются значения в сантиметрах), используем формулу расстояния между точками \(A(x_1;y_1)\) и \(B(x_2;y_2)\): \(AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\). Она берётся из теоремы Пифагора: разности координат дают катеты прямоугольного треугольника, а искомое расстояние — гипотенузу.

Для \(MK\): \(\Delta x=-3-(-7)=4\), \(\Delta y=5-(-5)=10\), значит \(MK=\sqrt{4^2+10^2}=\sqrt{16+100}=\sqrt{116}\approx 10{,}77\) (в единицах координатной сетки). Для \(KN\): \(\Delta x=7-(-3)=10\), \(\Delta y=1-5=-4\), значит \(KN=\sqrt{10^2+(-4)^2}=\sqrt{100+16}=\sqrt{116}\approx 10{,}77\). Для \(MN\): \(\Delta x=7-(-7)=14\), \(\Delta y=1-(-5)=6\), значит \(MN=\sqrt{14^2+6^2}=\sqrt{196+36}=\sqrt{232}\approx 15{,}23\).

В) Переход к значениям на чертеже в сантиметрах делается через масштаб сетки: измеряем линейкой длину одного деления (или заданного количества делений) и переводим длины в сантиметры. На рисунке после измерения получается \(MK\approx 5{,}4\) см и \(KN\approx 5{,}4\) см, то есть две стороны равны, а третья сторона \(MN\approx 7{,}6\) см — заметно больше.

Равенство \(MK\) и \(KN\) подтверждается и вычислениями: обе длины равны \(\sqrt{116}\) в координатных единицах. Значит, треугольник равнобедренный с равными боковыми сторонами \(MK\) и \(KN\), а основание — \(MN\). Это объясняет, почему на рисунке две стороны получились одинаковыми по линейке.

г) Углы можно измерить транспортиром прямо по построенному треугольнику: ставим центр транспортира в вершину, одну сторону совмещаем с нулевой линией и считываем градусную меру второй стороны. По рисунку видно, что угол при \(K\) прямой, то есть \(\angle K=90^\circ\).

Так как стороны \(MK\) и \(KN\) равны, то противоположные им углы равны: \(\angle M=\angle N\). Сумма углов треугольника равна \(180^\circ\), поэтому \(\angle M+\angle K+\angle N=180^\circ\). Подставляя \(\angle K=90^\circ\) и \(\angle M=\angle N\), получаем \(2\angle M+90^\circ=180^\circ\), значит \(\angle M=45^\circ\) и \(\angle N=45^\circ\), что совпадает с измерением на изображении.

д) Координаты середины отрезка \(MN\) находим по формуле середины: если \(M(x_M;y_M)\) и \(N(x_N;y_N)\), то середина \(S\) имеет координаты \(S\left(\frac{x_M+x_N}{2};\frac{y_M+y_N}{2}\right)\). Эта формула означает, что середина делит отрезок пополам и по \(x\), и по \(y\), поэтому берётся среднее арифметическое соответствующих координат.

Подставляем \(M(-7;-5)\) и \(N(7;1)\): \(x_S=\frac{-7+7}{2}=\frac{0}{2}=0\), \(y_S=\frac{-5+1}{2}=\frac{-4}{2}=-2\). Значит, середина стороны \(MN\) имеет координаты \((0;-2)\), что совпадает с указанным на рисунке результатом.