
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 656 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
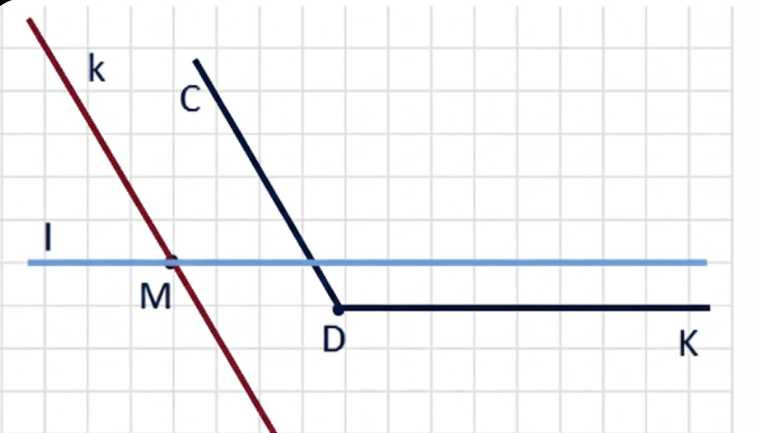
Начертите угол \(CDK\), равный \(130^\circ\). Отметьте точку \(M\), не лежащую на сторонах этого угла, и проведите через точку \(M\) прямые, параллельные сторонам угла \(CDK\).
Постройте угол \(CDK\) величиной \(130^\circ\) (лучи \(DC\) и \(DK\)).
Отметьте точку \(M\), не лежащую на лучах \(DC\) и \(DK\).
Через точку \(M\) проведите прямую \(k\), параллельную \(CD\), то есть \(k \parallel CD\).
Через точку \(M\) проведите прямую \(l\), параллельную \(DK\), то есть \(l \parallel DK\).
а) Сначала постройте угол \(CDK\) величиной \(130^\circ\). Для этого отметьте точку \(D\) (вершину угла), проведите из неё луч \(DK\) в удобном направлении, затем с помощью транспортира отложите от луча \(DK\) внутри угла \(130^\circ\) и проведите второй луч \(DC\). На концах лучей можно отметить точки \(K\) и \(C\), чтобы было видно, какая сторона угла где расположена, при этом важно, что стороны угла — это именно лучи \(DC\) и \(DK\), исходящие из точки \(D\).
Далее отметьте точку \(M\), которая не лежит на сторонах угла, то есть \(M\) не должна находиться ни на луче \(DC\), ни на луче \(DK\). Удобнее выбирать \(M\) внутри «сектора» между сторонами угла или снаружи, но в любом случае нужно следить, чтобы точка \(M\) не оказалась на самих сторонах: тогда через неё нельзя будет корректно показать две разные параллельные прямые к двум сторонам угла.
Затем через точку \(M\) проведите прямую \(k\), параллельную стороне \(CD\). Это означает, что вы строите прямую, имеющую то же направление, что и луч \(DC\): записывают \(k \parallel CD\). Практически это делается так: приложите линейку вдоль стороны \(CD\), зафиксируйте направление, затем, не меняя направления линейки (можно использовать угольник или метод «сдвига» линейки), перенесите её так, чтобы она проходила через точку \(M\), и проведите по линейке прямую \(k\).
После этого через ту же точку \(M\) проведите прямую \(l\), параллельную стороне \(DK\), то есть \(l \parallel DK\). Аналогично предыдущему шагу: ориентируйте линейку по стороне \(DK\), затем параллельным переносом расположите её так, чтобы линия проходила через \(M\), и проведите прямую \(l\). В итоге через \(M\) получаются две прямые, каждая параллельна своей стороне угла: \(k \parallel CD\) и \(l \parallel DK\), как на рисунке.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!