
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 649 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
Турист шёл в гору со скоростью \(3\) км/ч. Пройденный им путь можно вычислить по формуле \(s=3t\). Является ли зависимость пути, пройденного туристом, от времени прямой или обратной пропорциональной зависимостью? Составьте таблицу значений \(s\) для \(t=1; 2; 3; 4; 5\) ч. Постройте график движения туриста.
Зависимость пройденного пути от времени прямая пропорциональная, так как \(s=3t\), то есть \(s\) увеличивается в одинаковое число раз при увеличении \(t\) в одинаковое число раз.
| \(t\) | 1 | 2 | 3 | 4 | 5 |
| \(s\) | 3 | 6 | 9 | 12 | 15 |
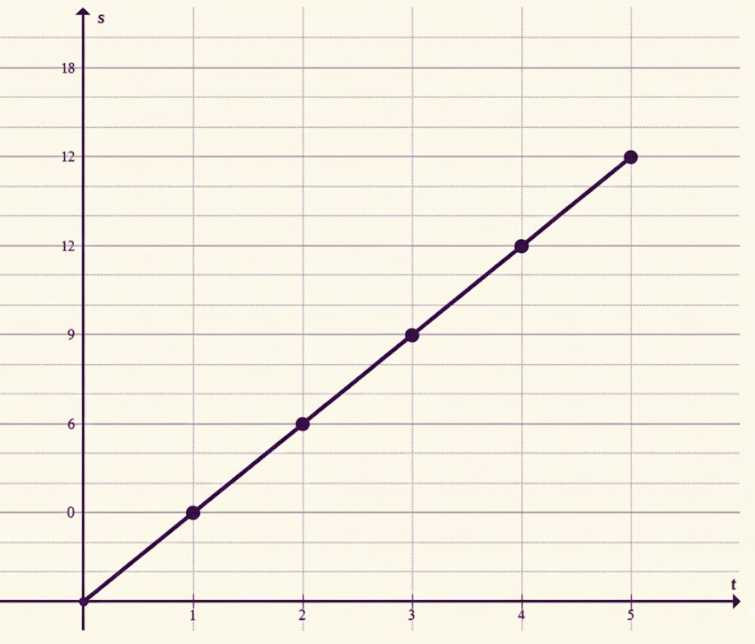
График — прямая \(s=3t\), проходящая через точки \((1;3)\), \((2;6)\), \((3;9)\), \((4;12)\), \((5;15)\) и начало координат \((0;0)\).
а) Зависимость пути \(s\) от времени \(t\) является прямой пропорциональной, потому что путь при равномерном движении вычисляется по формуле \(s=vt\), а в задаче скорость постоянна и равна \(v=3\) км/ч. Значит, для любого времени \(t\) значение пути \(s\) получается умножением \(t\) на одно и то же число 3, то есть \(s=3t\).
Это и есть признак прямой пропорциональности: отношение \(\frac{s}{t}\) постоянно и равно 3 (при \(t\neq 0\)). Если увеличить время, например, в 2 раза, то и путь увеличится в 2 раза, потому что в формуле \(s=3t\) переменная \(t\) стоит в первой степени и умножается на постоянный коэффициент.
б) Для таблицы значений подставляем заданные значения времени \(t=1,2,3,4,5\) в формулу \(s=3t\) и каждый раз умножаем \(t\) на 3. Например, при \(t=1\) получаем \(s=3\cdot 1=3\), при \(t=2\) получаем \(s=3\cdot 2=6\).
Аналогично: при \(t=3\) \(s=3\cdot 3=9\), при \(t=4\) \(s=3\cdot 4=12\), при \(t=5\) \(s=3\cdot 5=15\). Эти значения показывают, что за каждый следующий час турист проходит на 3 км больше, потому что скорость постоянна \(3\) км/ч.
| \(t\) | 1 | 2 | 3 | 4 | 5 |
| \(s\) | 3 | 6 | 9 | 12 | 15 |
в) Чтобы построить график движения, по оси \(t\) откладываем время (в часах), а по оси \(s\) — путь (в километрах). Для построения берём точки из таблицы: \((1;3)\), \((2;6)\), \((3;9)\), \((4;12)\), \((5;15)\) и наносим их на координатную плоскость.
Затем соединяем отмеченные точки прямой линией, так как зависимость задаётся линейной формулой \(s=3t\). Эта прямая проходит через начало координат \((0;0)\), поскольку при \(t=0\) по формуле \(s=3\cdot 0=0\), то есть в момент начала движения пройденный путь равен нулю.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!