ГДЗ по Математике 6 Класс Часть 2 Номер 648 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

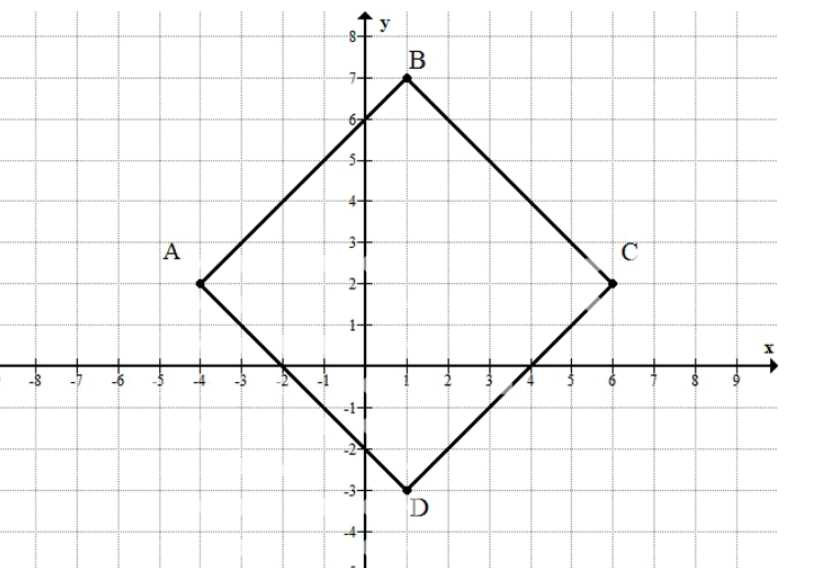
Отметьте на координатной плоскости вершины \(A(-4; 2)\), \(B(1; 7)\) и \(C(6; 2)\) квадрата \(ABCD\). Найдите координаты вершины \(D\).

Так как \(ABCD\) — квадрат, то это параллелограмм, и выполняется векторное равенство \( \vec{AD}=\vec{BC}\), поэтому \(D=A+C-B\).

\(D=(-4,2)+(6,2)-(1,7)=(1,-3)\).

а) Так как дан квадрат \(ABCD\), то он является параллелограммом: противоположные стороны параллельны и равны как векторы. Это означает, что вектор \(\vec{AD}\) равен вектору \(\vec{BC}\), потому что стороны \(AD\) и \(BC\) — противоположные (параллельные) стороны параллелограмма, а направление обхода вершин \(A \to B \to C \to D\) сохраняет согласованность направлений векторов.

Найдём \(\vec{BC}\) по координатам точек \(B(1;7)\) и \(C(6;2)\): \(\vec{BC}=(6-1;\,2-7)=(5;\,-5)\). Тогда \(\vec{AD}=(5;\,-5)\), а значит координаты точки \(D\) получаются прибавлением этого вектора к точке \(A(-4;2)\): \(D=A+\vec{AD}=(-4+5;\,2-5)=(1;\,-3)\).

То же самое можно записать одной формулой для параллелограмма: \(D=A+C-B\). Подставляя координаты \(A(-4;2)\), \(B(1;7)\), \(C(6;2)\), получаем \(D=(-4;2)+(6;2)-(1;7)=(1;\,-3)\), что совпадает с расположением вершины \(D\) на рисунке (под точкой \(B\) по \(x\) и симметрично относительно середины диагоналей).