ГДЗ по Математике 6 Класс Часть 2 Номер 646 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

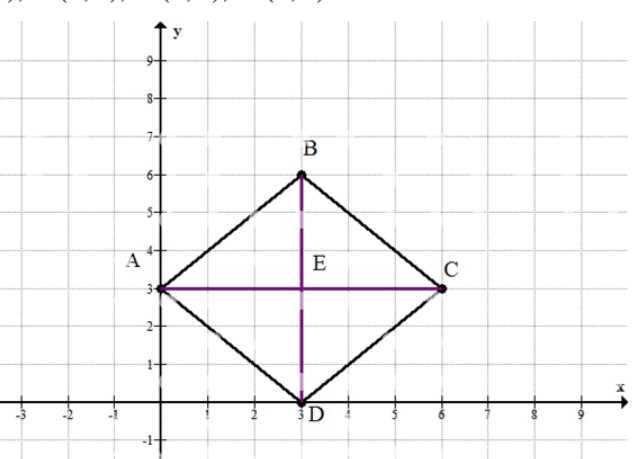
Постройте квадрат \(ABCD\) по координатам его вершин \(A(0; 3)\), \(B(3; 6)\), \(C(6; 3)\) и \(D(3; 0)\). Проведите отрезки \(AC\) и \(BD\). Найдите координаты точки, в которой пересекаются эти отрезки.

Точка пересечения диагоналей квадрата — середина каждой диагонали, значит \(E\) — середина \(AC\).

Середина \(AC\): \(E\left(\frac{0+6}{2};\frac{3+3}{2}\right)=(3;3)\).

Ответ: \(E(3;3)\).

Диагонали квадрата \(AC\) и \(BD\) пересекаются в одной точке, которая одновременно является серединой каждой диагонали. Это свойство квадрата: диагонали в нём взаимно перпендикулярны и делят друг друга пополам, поэтому точка пересечения находится ровно посередине между концами любой диагонали.

Удобнее всего найти эту точку как середину диагонали \(AC\), потому что координаты точек \(A(0;3)\) и \(C(6;3)\) даны. Координаты середины отрезка с концами \(A(x_A;y_A)\) и \(C(x_C;y_C)\) находятся по формуле \(E\left(\frac{x_A+x_C}{2};\frac{y_A+y_C}{2}\right)\), так как по оси \(x\) и по оси \(y\) берутся средние арифметические соответствующих координат.

Подставляем значения: \(E\left(\frac{0+6}{2};\frac{3+3}{2}\right)\). Получаем \(E\left(\frac{6}{2};\frac{6}{2}\right)=(3;3)\), то есть точка пересечения диагоналей имеет координаты \(E(3;3)\). Это совпадает с рисунком: диагональ \(AC\) горизонтальна на уровне \(y=3\), а диагональ \(BD\) вертикальна при \(x=3\), поэтому их пересечение находится в точке \((3;3)\).