ГДЗ по Математике 6 Класс Часть 2 Номер 645 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

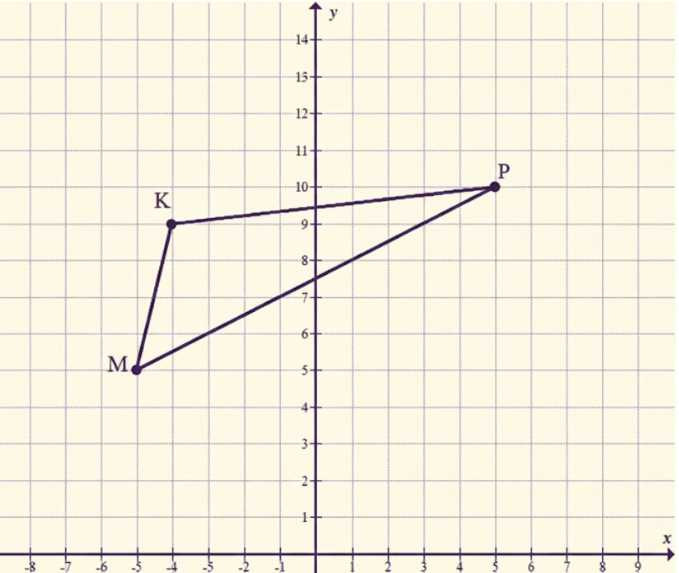
На координатной плоскости начертите треугольник \(MKP\), если \(M(-5; 5)\), \(K(-4; 9)\), \(P(5; 10)\). Измерьте транспортиром углы этого треугольника.

Отметьте на координатной плоскости точки \(M(-5;5)\), \(K(-4;9)\), \(P(5;10)\) и соедините их отрезками \(MK\), \(KP\), \(PM\), получив треугольник \(MKP\).

Измерьте транспортиром углы при вершинах \(M\), \(K\), \(P\).

Получается: \(\angle M=49^\circ\), \(\angle K=110^\circ\), \(\angle P=21^\circ\).

Отметьте на координатной плоскости точку \(M(-5;5)\): от начала координат переместитесь на \(5\) клеток влево по оси \(x\) (так как \(x=-5\)), затем на \(5\) клеток вверх по оси \(y\) (так как \(y=5\)). Аналогично отметьте точку \(K(-4;9)\): на \(4\) клетки влево и на \(9\) клеток вверх, и точку \(P(5;10)\): на \(5\) клеток вправо и на \(10\) клеток вверх. Важно аккуратно поставить точки именно в узлах сетки, потому что небольшая ошибка в положении точки заметно меняет измеряемые транспортиром углы.

Соедините точки отрезками \(MK\), \(KP\) и \(PM\), чтобы получился треугольник \(MKP\). Удобно проводить отрезки по линейке, чтобы стороны были прямыми: сначала соедините \(M\) с \(K\), затем \(K\) с \(P\), затем \(P\) с \(M\). После построения проверьте, что вершины подписаны верно и что стороны сходятся точно в точках \(M\), \(K\), \(P\), иначе при измерении возникнет погрешность.

Для измерения угла \(\angle M\) приложите транспортир так, чтобы его центр совпал с точкой \(M\), а нулевая линия транспортира легла вдоль одной из сторон, например вдоль \(MK\). Затем, не сдвигая транспортир, посмотрите, на каком делении шкалы пересекает транспортир вторая сторона \(MP\): получаете величину \(\angle M=49^\circ\). Аналогично измерьте \(\angle K\): центр транспортира в точке \(K\), нулевую линию совместите с \(KM\) или \(KP\), а по пересечению со второй стороной получите \(\angle K=110^\circ\). Точно так же измерьте \(\angle P\): центр в точке \(P\), нулевая линия вдоль \(PK\) или \(PM\), по второй стороне считываете \(\angle P=21^\circ\).

При измерениях следите, чтобы вы выбирали правильную шкалу транспортира: если основание совмещено со стороной, то отсчет нужно вести от \(0^\circ\), лежащего на этой стороне, а не от противоположного \(180^\circ\). Для самопроверки можно использовать факт, что сумма углов треугольника равна \(180^\circ\): \(49^\circ+110^\circ+21^\circ=180^\circ\), значит измерения согласованы. Итоговые значения, как на рисунке: \(\angle M=49^\circ\), \(\angle K=110^\circ\), \(\angle P=21^\circ\).