ГДЗ по Математике 6 Класс Часть 2 Номер 643 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

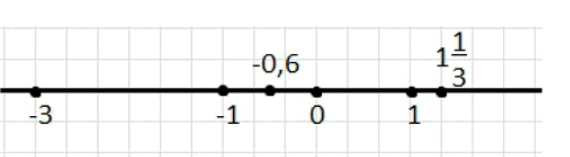
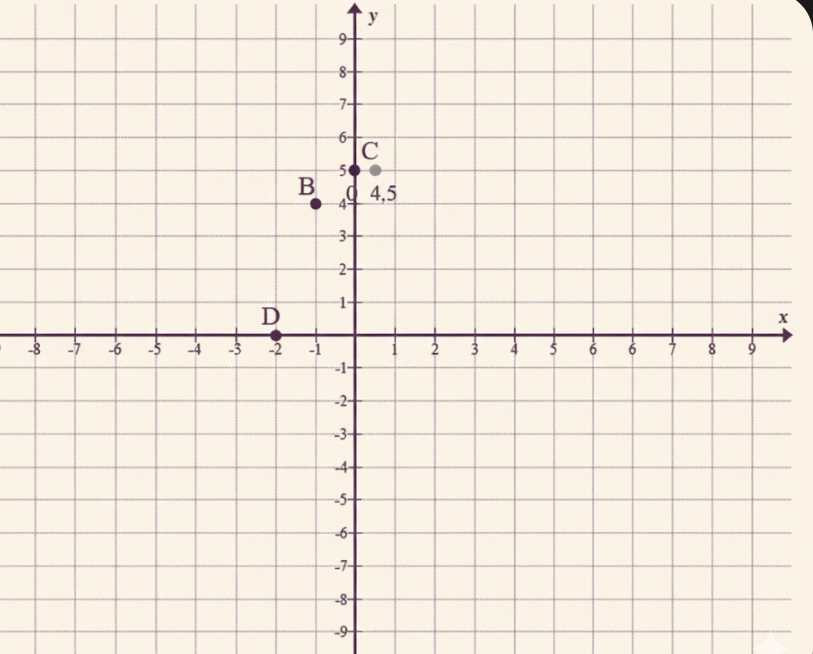
Постройте точки: а) на координатной прямой: \(M(-3)\), \(K(1\frac{1}{3})\), \(P(-0{,}6)\); б) на координатной плоскости: \(B(-1; 4)\), \(C(0; 5)\), \(D(-2; 0)\). В упражнении б) назовите абсциссу и ординату каждой точки.

а) На координатной прямой отмечаем точки по их координатам: \(M(-3)\) — в точке \(-3\), \(P(-0{,}6)\) — между \(-1\) и \(0\) ближе к \(0\), \(K(1\frac{1}{3})\) — правее \(1\) на \( \frac{1}{3}\) (то есть \(K(\frac{4}{3})\)).

б) На координатной плоскости: точка \(B(-1;4)\) — абсцисса \(-1\), ордината \(4\); точка \(C(0;5)\) — абсцисса \(0\), ордината \(5\); точка \(D(-2;0)\) — абсцисса \(-2\), ордината \(0\).

а) На координатной прямой каждая точка задаётся одним числом — её координатой. Чтобы отметить точку, сначала находим на прямой нужные целые числа, а затем учитываем знак и величину числа: отрицательные координаты располагаются слева от \(0\), положительные — справа от \(0\). Чем меньше число, тем левее точка, чем больше — тем правее.

Точка \(M(-3)\) ставится ровно в делении \(-3\), так как координата целая и дополнительного деления отрезка не требуется. Точка \(P(-0{,}6)\) имеет координату между \(-1\) и \(0\): это число отрицательное, значит точка лежит слева от \(0\), и по модулю меньше \(1\), значит она находится ближе к \(0\), чем к \(-1\). Точку \(K(1\frac{1}{3})\) отмечаем справа от \(1\), потому что \(1\frac{1}{3}>1\); дробная часть \(\frac{1}{3}\) означает, что отрезок от \(1\) до \(2\) нужно мысленно разделить на \(3\) равные части и взять первую часть от \(1\) вправо, то есть \(K\) находится в точке \(1+\frac{1}{3}\).

б) На координатной плоскости положение точки задаётся парой чисел \((x;y)\), где \(x\) — абсцисса (координата по оси \(x\), горизонталь), а \(y\) — ордината (координата по оси \(y\), вертикаль). Чтобы построить точку \((x;y)\), сначала от \(0\) на оси \(x\) откладывают \(x\): вправо, если \(x>0\), и влево, если \(x<0\); затем из полученной точки поднимаются или опускаются параллельно оси \(y\) на величину \(y\): вверх, если \(y>0\), и вниз, если \(y<0\). Для точки \(B(-1;4)\) абсцисса равна \(-1\), значит от начала координат по оси \(x\) нужно сделать один шаг влево до \(x=-1\); затем ордината \(4\) означает подняться вверх на \(4\) единицы до уровня \(y=4\). Для точки \(C(0;5)\) абсцисса \(0\) показывает, что точка лежит прямо на оси \(y\); далее ордината \(5\) задаёт подъём вверх на \(5\) единиц, поэтому точка находится на оси \(y\) на уровне \(y=5\). Для точки \(D(-2;0)\) абсцисса \(-2\) означает два шага влево по оси \(x\) до \(x=-2\), а ордината \(0\) показывает, что точка лежит на оси \(x\), так как подъёма или спуска нет, то есть \(y=0\).