ГДЗ по Математике 6 Класс Часть 2 Номер 596 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

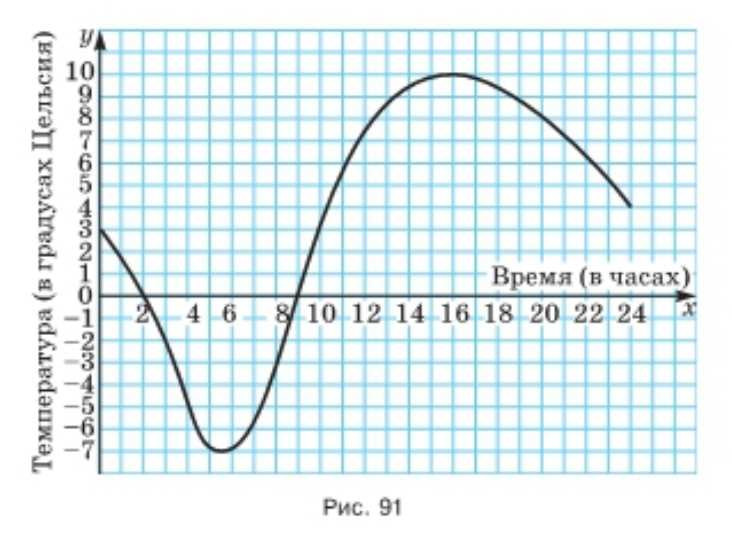
На рисунке 91 изображён график изменения температуры воздуха в течение суток. Определите по графику:

а) температуру воздуха в \(4\ \text{ч}\); в \(14\ \text{ч}\); в \(22\ \text{ч}\);

б) время суток, когда температура воздуха была равна \(0\ ^\circ\mathrm{C}\); \(5\ ^\circ\mathrm{C}\); \(-3\ ^\circ\mathrm{C}\);

в) промежутки времени, когда температура воздуха повышалась; понижалась;

г) промежутки времени, когда температура воздуха была положительной; отрицательной.

а) По графику считываем значения температуры в указанные моменты времени: в \(4\) ч \(T=-5^\circ C\), в \(14\) ч \(T=9{,}5^\circ C\), в \(22\) ч \(T=6{,}3^\circ C\).

б) Находим по графику моменты времени, когда температура принимает заданные значения: \(T=0^\circ C\) в \(2\) ч и в \(9\) ч; \(T=5^\circ C\) в \(10\) ч \(30\) мин и в \(23\) ч; \(T=-3^\circ C\) в \(3\) ч \(30\) мин и в \(8\) ч.

в) Температура повышалась на участке, где график идёт вверх: с \(5\) ч \(30\) мин до \(16\) ч; понижалась на участках, где график идёт вниз: с \(0\) ч до \(5\) ч \(30\) мин и с \(16\) ч до \(24\) ч.

г) Температура положительная там, где график выше оси \(T=0\): с \(0\) ч до \(2\) ч и с \(9\) ч до \(24\) ч; отрицательная там, где график ниже оси \(T=0\): с \(2\) ч до \(9\) ч.

а) Чтобы ответить, в каждый указанный момент времени мысленно проводим на графике вертикальную линию через нужный час и смотрим, на каком уровне по шкале температур находится точка графика. Это и есть значение \(T\) в данный момент: время берётся по горизонтальной оси, температура — по вертикальной, поэтому координаты точки читаются как \((t,\,T)\).

При \(t=4\) ч точка графика находится на уровне \(-5^\circ C\), значит \(T=-5^\circ C\). При \(t=14\) ч точка лежит на уровне \(9{,}5^\circ C\), поэтому \(T=9{,}5^\circ C\). При \(t=22\) ч график соответствует \(6{,}3^\circ C\), то есть \(T=6{,}3^\circ C\). Эти значения просто считываются с графика по пересечению вертикали \(t=\) заданное время с линией температуры.

б) Здесь делаем обратное действие: задано значение температуры, значит находим на графике горизонтальный уровень \(T=\) нужное число и ищем все места, где график этот уровень пересекает. Каждому пересечению соответствует момент времени, который читаем по горизонтальной оси, потому что в точках пересечения выполняется условие \(T\) равно заданному значению.

Для \(T=0^\circ C\) уровень совпадает с осью нуля, и график пересекает его в двух местах: в \(2\) ч и в \(9\) ч, значит температура была \(0^\circ C\) именно тогда. Для \(T=5^\circ C\) проводим горизонталь на высоте \(5^\circ C\) и видим пересечения в \(10\) ч \(30\) мин и в \(23\) ч, следовательно в эти моменты \(T=5^\circ C\). Для \(T=-3^\circ C\) берём уровень \(-3^\circ C\): график даёт пересечения в \(3\) ч \(30\) мин и в \(8\) ч, значит именно в эти два времени температура равнялась \(-3^\circ C\).

в) Повышение температуры на графике соответствует участку, где линия идёт вверх при движении слева направо: с ростом времени \(t\) температура \(T\) становится больше. Понижение — там, где линия идёт вниз: при увеличении \(t\) значение \(T\) уменьшается. Поэтому достаточно определить промежутки времени, на которых наклон графика положительный (рост) и отрицательный (убывание).

По графику видно, что после \(5\) ч \(30\) мин линия начинает подниматься и продолжает подниматься до \(16\) ч, значит на промежутке от \(5\) ч \(30\) мин до \(16\) ч температура повышалась. До этого, от \(0\) ч до \(5\) ч \(30\) мин, график идёт вниз, поэтому температура понижалась на промежутке от \(0\) ч до \(5\) ч \(30\) мин. После \(16\) ч линия снова направлена вниз до конца суток, значит температура понижалась также с \(16\) ч до \(24\) ч.

г) Положительная температура означает \(T>0^\circ C\), то есть график расположен выше линии \(T=0^\circ C\). Отрицательная температура означает \(T<0^\circ C\), то есть график ниже линии \(T=0^\circ C\). Поэтому нужно найти промежутки времени, где график находится выше или ниже нулевого уровня, а границы этих промежутков задаются точками пересечения с \(T=0^\circ C\).

По графику пересечения с уровнем \(T=0^\circ C\) происходят в \(2\) ч и в \(9\) ч. С \(0\) ч до \(2\) ч график расположен выше нуля, значит температура положительная на промежутке \(0\) ч–\(2\) ч. Между \(2\) ч и \(9\) ч график ниже нулевой линии, значит температура отрицательная с \(2\) ч до \(9\) ч. Начиная с \(9\) ч и до \(24\) ч график снова выше \(T=0^\circ C\), поэтому температура положительная с \(9\) ч до \(24\) ч.