ГДЗ по Математике 6 Класс Часть 2 Номер 593 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

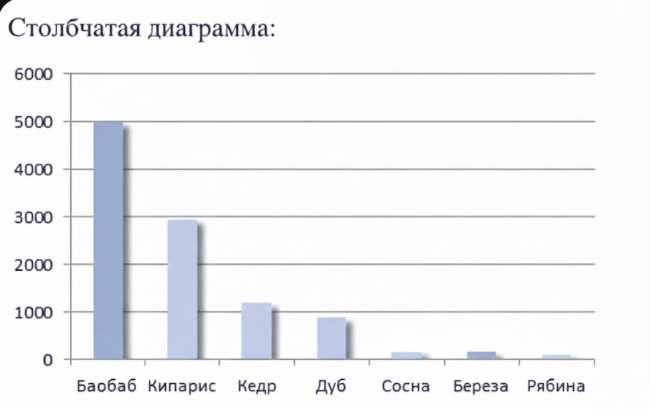
Постройте столбчатую диаграмму сравнительной продолжительности жизни некоторых деревьев по следующим данным: баобаб — \(5000\) лет, кипарис — \(3000\) лет, кедр — \(1200\) лет, дуб — \(1000\) лет, сосна обыкновенная — \(600\) лет, берёза — \(250\) лет, рябина — \(80\) лет.

По оси \(Ox\) отметьте названия деревьев: баобаб, кипарис, кедр, дуб, сосна, берёза, рябина. По оси \(Oy\) отложите продолжительность жизни в годах, выберите масштаб от \(0\) до \(6000\) с шагом \(1000\).

Постройте столбцы до соответствующих значений: баобаб — \(5000\), кипарис — \(3000\), кедр — \(1200\), дуб — \(1000\), сосна — \(600\), берёза — \(250\), рябина — \(80\). Высота каждого столбца равна числу лет по выбранному масштабу.

а) Переместительное свойство сложения записывают так: \(a+b=b+a\). Оно означает, что при сложении можно менять местами слагаемые, и значение суммы от этого не изменится. Поэтому, если удобнее сначала сложить другие числа, их можно переставить без ошибки.

Сочетательное свойство сложения записывают так: \(a+(b+c)=(a+b)+c\). Оно означает, что при сложении трёх и более чисел можно по-разному расставлять скобки (то есть менять порядок выполнения сложения), и итоговая сумма будет той же. Это позволяет выбирать более удобные пары для вычислений.

В примере сначала удобно сгруппировать числа, которые дают «круглое» значение: \(2{,}5+(0{,}5+1{,}8)=(2{,}5+0{,}5)+1{,}8\). Здесь применили сочетательное свойство, чтобы перенести скобки и первым действием сложить \(2{,}5\) и \(0{,}5\).

Дальше выполняем вычисления по шагам: \(2{,}5+0{,}5=3\), затем \(3+1{,}8=4{,}8\). Получаем \(2{,}5+(0{,}5+1{,}8)=4{,}8\), что показывает, что перестановка скобок не изменила результат, а только упростила счёт.

б) Переместительное свойство умножения записывают так: \(ab=ba\). Оно означает, что при умножении множители можно менять местами, и произведение останется тем же. Это полезно, когда хочется сначала перемножить те числа, которые дают простой результат.

Сочетательное свойство умножения записывают так: \(a(bc)=(ab)c\). Оно означает, что при умножении трёх чисел можно по-разному расставлять скобки, то есть выбирать, какие два множителя перемножить первыми, и итог не изменится. Благодаря этому можно группировать множители так, чтобы вычисления были проще.

В примере удобно сначала перемножить \(0{,}2\) и \(5\), потому что это даёт единицу: \(0{,}2\cdot(5\cdot0{,}3)=(0{,}2\cdot5)\cdot0{,}3\). Здесь применили сочетательное свойство, чтобы изменить группировку множителей.

Далее считаем: \(0{,}2\cdot5=1\), после чего остаётся \(1\cdot0{,}3=0{,}3\). Получаем \(0{,}2\cdot(5\cdot0{,}3)=0{,}3\), то есть перенос скобок и удобная группировка не меняют произведение, а только упрощают вычисление.

в) Свойство \(a+0=a\) означает, что прибавление нуля не изменяет число: к любому числу добавили «ничего», поэтому оно остаётся тем же. Это правило работает для любых чисел и часто используется при упрощении выражений.

Свойство \(a+(-a)=0\) означает, что сумма противоположных чисел равна нулю. Числа \(a\) и \(-a\) имеют одинаковые модули, но противоположные знаки, поэтому при сложении полностью взаимно уничтожаются, и результат равен нулю.

Поэтому в примере \(5+0=5\): ноль не влияет на значение числа. Это прямое применение правила \(a+0=a\) при \(a=5\).

Аналогично \(5+(-5)=0\): числа \(5\) и \(-5\) противоположны, значит их сумма равна нулю. Это частный случай правила \(a+(-a)=0\) при \(a=5\).

г) Свойство \(a\cdot0=0\) означает, что умножение на нуль даёт нуль. Интуитивно это можно понимать так: если взять \(0\) групп по \(a\) (или \(a\) групп по \(0\)), то в итоге ничего не получится, то есть результат будет \(0\).

Свойство \(a\cdot1=a\) означает, что умножение на единицу не изменяет число. Единица — это нейтральный множитель: число берётся ровно один раз, поэтому остаётся тем же.

Свойство \(a\cdot\frac{1}{a}=1,\ a\ne0\) означает, что число, умноженное на обратное ему число, даёт \(1\). Ограничение \(a\ne0\) нужно потому, что обратное число \(\frac{1}{a}\) существует только для ненулевых \(a\).

Поэтому в примерах получаем: \(5\cdot0=0\), так как любое число при умножении на \(0\) даёт \(0\). Далее \(5\cdot1=5\), так как умножение на \(1\) не меняет число.

И наконец, \(5\cdot\frac{1}{5}=1\), потому что \(\frac{1}{5}\) — число, обратное \(5\), и их произведение равно \(1\). Здесь условие \(a\ne0\) выполнено, так как \(5\ne0\).