ГДЗ по Математике 6 Класс Часть 2 Номер 572 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

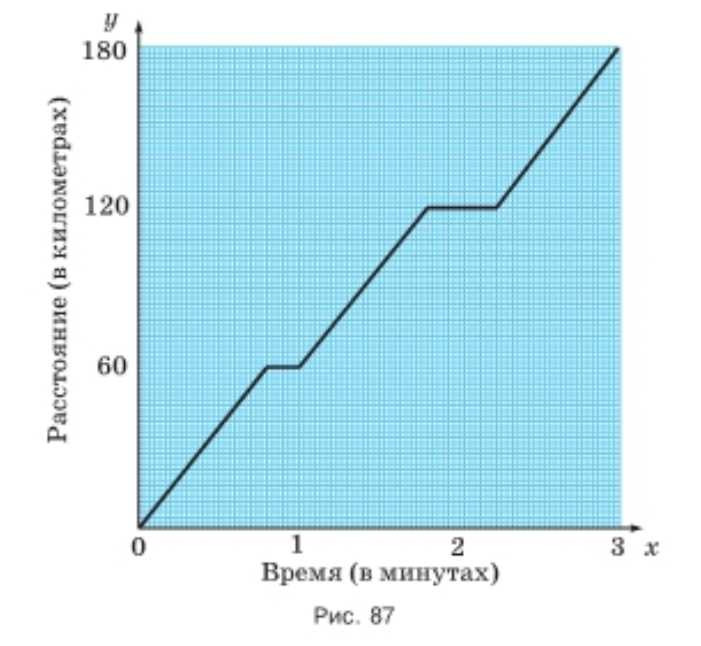
На рисунке 87 изображён график движения поезда. Определите по графику:

а) какое расстояние прошёл поезд за первые 2 ч;

б) сколько минут поезд стоял на каждой остановке;

в) каково расстояние между остановками поезда;

г) среднюю скорость движения за 3 ч.

а) За первые \(2\) ч поезд прошёл \(120\) км.

б) На первой остановке поезд стоял \(14\) мин, на второй остановке поезд стоял \(28\) мин.

в) Между остановками поезда расстояние \(60\) км.

г) Средняя скорость движения за \(3\) ч: \(180 : 3 = 60\) (км/ч).

а) Из условия известно, что за первые \(2\) часа поезд прошёл \(120\) км. Это означает, что за указанный промежуток времени уже определено пройденное расстояние, и его не нужно вычислять по скорости или по графику — значение дано напрямую.

Запись «за первые \(2\) ч — \(120\) км» фиксирует результат для начального участка движения: время берём \(2\) ч, а расстояние к этому моменту равно \(120\) км. Поэтому в ответе по этому пункту остаётся указать именно эти данные без дополнительных преобразований.

б) По условию на первой остановке поезд стоял \(14\) минут, а на второй остановке — \(28\) минут. Здесь речь идёт не о движении, а о времени стоянки, поэтому расстояние в эти промежутки не увеличивается, а время поездки при подсчётах общего времени учитывается.

Так как величины уже заданы, задача в этом пункте сводится к корректной фиксации: первая стоянка \(14\) мин, вторая стоянка \(28\) мин. При необходимости дальнейших расчётов важно помнить, что это минуты, и перевод в часы делается по правилу \(1\) ч \(= 60\) мин (например, \(14\) мин \(= \frac{14}{60}\) ч, \(28\) мин \(= \frac{28}{60}\) ч), но в данном пункте достаточно указать данные как есть.

в) Указано, что между остановками поезда расстояние \(60\) км. Это означает, что участок пути от одной остановки до следующей имеет длину \(60\) км, и именно это значение используется при анализе перемещений между остановками.

Поскольку расстояние дано непосредственно, дополнительных вычислений не требуется: между остановками поезд проходит \(60\) км. В дальнейшем это может применяться, например, для нахождения скорости на перегоне по формуле \(v = \frac{s}{t}\), где \(s = 60\) км, но в рамках данного пункта достаточно зафиксировать указанное расстояние.

г) Для средней скорости за \(3\) часа берём общий путь за эти \(3\) часа, который равен \(180\) км (как в записи на фото), и делим на общее время движения \(3\) часа. Используется стандартная формула средней скорости \(v_{\text{ср}} = \frac{s}{t}\).

Подставляем значения: \(v_{\text{ср}} = \frac{180}{3} = 60\). В записи из условия это оформлено как \(180 : 3 = 60\) (км/ч), то есть средняя скорость движения за \(3\) часа равна \(60\) км/ч.