ГДЗ по Математике 6 Класс Часть 2 Номер 566 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

Начертите на координатной плоскости такой отрезок, чтобы абсциссы и ординаты его точек удовлетворяли условиям:

а) \(-2\le x\le 5,\ -3\le y\le 7\); б) \(|x|<6,\ |y|<4\).

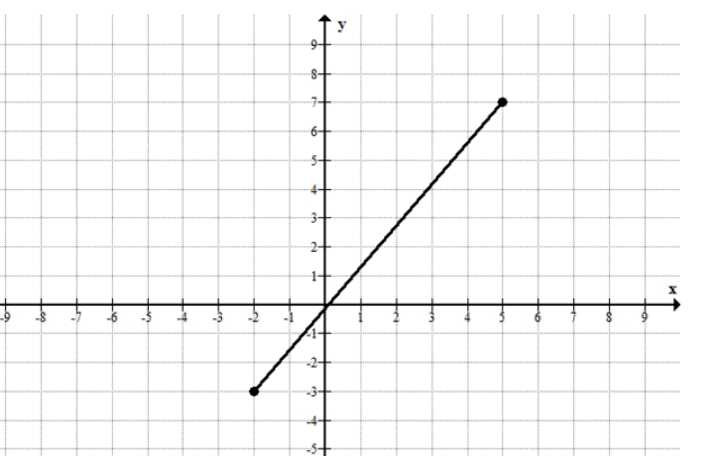
а) Берём крайние значения: при \(x=-2\) имеем \(y=-3\), при \(x=5\) имеем \(y=7\). Начертить отрезок с концами \((-2,-3)\) и \((5,7)\).

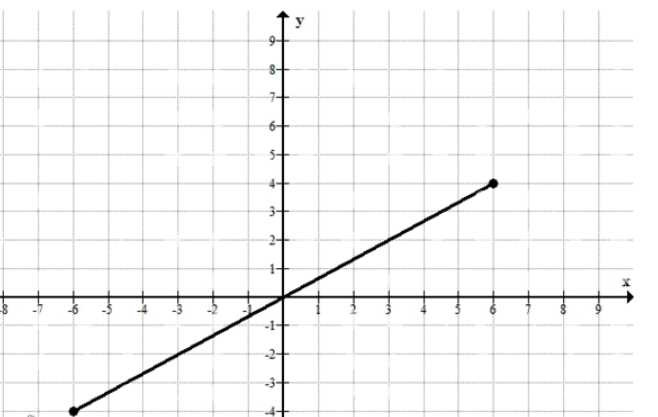
б) Так как \(|x|\le 6\Rightarrow -6\le x\le 6\) и \(|y|\le 4\Rightarrow -4\le y\le 4\), берём крайние точки \((-6,-4)\) и \((6,4)\). Начертить отрезок с концами \((-6,-4)\) и \((6,4)\).

а) Условия \(-2\le x\le 5\) и \(-3\le y\le 7\) означают, что для любой точки отрезка её абсцисса должна быть не меньше \(-2\) и не больше \(5\), а ордината — не меньше \(-3\) и не больше \(7\). Чтобы построить именно отрезок, удобно взять две точки с координатами, равными «крайним» допустимым значениям, чтобы весь отрезок располагался внутри заданных промежутков по \(x\) и по \(y\).

Берём точку \(A(-2,-3)\): её координаты удовлетворяют условиям, так как \(-2\) — это левый конец промежутка для \(x\), а \(-3\) — нижний конец промежутка для \(y\). Берём точку \(B(5,7)\): её координаты тоже допустимы, так как \(5\) — правый конец промежутка для \(x\), а \(7\) — верхний конец промежутка для \(y\).

Соединяем \(A\) и \(B\) прямой линией — получаем отрезок \(AB\). Для любой точки этого отрезка координаты изменяются между координатами концов: абсцисса будет лежать между \(-2\) и \(5\), то есть \(-2\le x\le 5\), а ордината — между \(-3\) и \(7\), то есть \(-3\le y\le 7\). Поэтому отрезок с концами \((-2,-3)\) и \((5,7)\) соответствует требованию и совпадает с рисунком.

б) Неравенства \(|x|\le 6\) и \(|y|\le 4\) задают ограничения на координаты по модулю: абсцисса любой точки по абсолютному значению не превосходит \(6\), а ордината по абсолютному значению не превосходит \(4\). Это равносильно записи промежутков \(-6\le x\le 6\) и \(-4\le y\le 4\), то есть точки должны лежать в прямоугольнике с границами \(x=-6\), \(x=6\), \(y=-4\), \(y=4\).

Чтобы построить подходящий отрезок, берём две точки, у которых координаты одновременно достигают крайних допустимых значений по обоим осям. Тогда весь соединяющий их отрезок будет проходить внутри указанного прямоугольника, а координаты всех его точек будут оставаться в нужных пределах.

Выбираем \(C(-6,-4)\) и \(D(6,4)\). У точки \(C\) выполняется \(|-6|=6\) и \(|-4|=4\), у точки \(D\) выполняется \(|6|=6\) и \(|4|=4\), значит обе точки удовлетворяют ограничениям. Соединяем \(C\) и \(D\) — получаем отрезок с концами \((-6,-4)\) и \((6,4)\); на нём абсциссы меняются от \(-6\) до \(6\), а ординаты — от \(-4\) до \(4\), поэтому для любой его точки выполняется \(|x|\le 6\) и \(|y|\le 4\), как на рисунке.