ГДЗ по Математике 6 Класс Часть 2 Номер 557 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

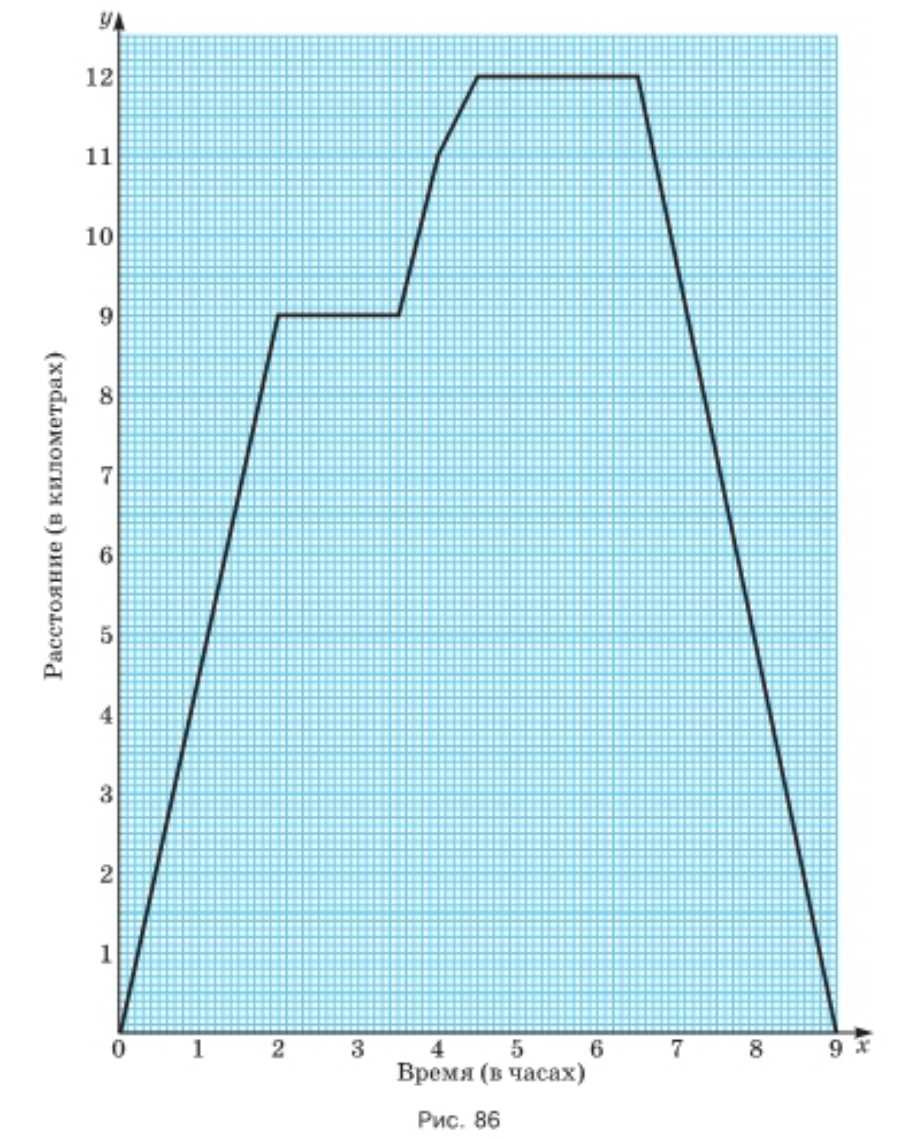
Рыболов рассказал, что, выйдя из дома, он шёл 2 ч по берегу реки и дошёл до места, где в неё впадает приток. Там он ловил рыбу 1,5 ч, а потом пошёл дальше. Через 1 ч он выбрал новое место, где в течение 2 ч ловил рыбу, варил уху, обедал. После обеда он отправился домой. На всё это он затратил 9 ч. График движения рыболова изображён на рисунке 86. Ответьте на следующие вопросы.
а) На каком расстоянии от дома был рыболов через 30 мин; через 4 ч 40 мин; через 5,5 ч после выхода из дома?
б) Через сколько часов после выхода из дома был рыболов в 5 км от дома?
в) Когда расстояние от дома увеличивалось; уменьшалось; не изменялось?
г) Сколько километров прошёл рыболов за последние 2 ч?
д) С какой скоростью рыболов шёл в первый и с какой в последний час пути? Чему равна скорость движения рыболова в промежутке времени между 4 и 4,5 ч после выхода из дома?

а) По графику расстояния: через \(30\) мин \(S=2\) км; через \(4\) ч \(40\) мин \(S=12\) км; через \(5\) ч \(30\) мин \(S=12\) км.

б) По графику уровень \(S=5\) км достигается при \(t=1\) ч \(10\) мин.

в) Увеличение там, где график идет вверх: с \(0\) ч до \(2\) ч и с \(3\) ч \(30\) мин до \(4\) ч \(30\) мин.
Уменьшение там, где график идет вниз: с \(6\) ч \(30\) мин до \(9\) ч.
Постоянно там, где график горизонтален: с \(2\) ч до \(3\) ч \(30\) мин и с \(4\) ч \(30\) мин до \(6\) ч \(30\) мин.

г) За последние \(2\) часа по графику пройдено \(9{,}5\) км.

д) За первый час пройдено \(4{,}5\) км, значит скорость \(v=\frac{4{,}5}{1}=4{,}5\) км/ч; за последний час пройдено \(4{,}5\) км, значит \(v=\frac{4{,}5}{1}=4{,}5\) км/ч.
В \(4\) ч \(S=11\) км, в \(4{,}5\) ч \(S=12\) км, значит за \(30\) мин прошел \(1\) км, скорость \(v=\frac{1}{0{,}5}=2\) км/ч.

а) Смотрим на график зависимости расстояния от дома \(S\) (в км) от времени \(t\) (в часах и минутах) и просто считываем значения в указанные моменты времени. В момент \(t=30\) мин отмеченная точка графика соответствует расстоянию \(S=2\) км, значит через \(30\) минут рыболов находился в \(2\) км от дома.

Далее считываем значения в моменты \(t=4\) ч \(40\) мин и \(t=5\) ч \(30\) мин. На графике в \(4\) ч \(40\) мин расстояние равно \(12\) км, то есть \(S=12\) км; и в \(5\) ч \(30\) мин график по-прежнему показывает \(12\) км, значит \(S=12\) км и во второй момент. Это согласуется с горизонтальным участком графика на уровне \(12\) км: расстояние на нем не меняется, поэтому в разные моменты внутри этого участка получается одно и то же значение \(S\).

б) Нужно найти момент времени, когда расстояние от дома равно \(5\) км, то есть решить по графику задачу «когда \(S=5\)». Для этого находим на оси расстояний уровень \(S=5\) км и смотрим, где график пересекает этот уровень.

Точка пересечения соответствует времени \(t=1\) ч \(10\) мин. Значит рыболов был в \(5\) км от дома через \(1\) час \(10\) минут, потому что именно в этот момент график показывает значение \(S=5\) км.

в) Увеличение расстояния означает, что рыболов удаляется от дома, а на графике это видно как участок, где линия идет вверх при движении слева направо (с ростом времени). Поэтому выделяем все промежутки времени, на которых график возрастает: с \(0\) ч до \(2\) ч и с \(3\) ч \(30\) мин до \(4\) ч \(30\) мин.

Уменьшение расстояния означает, что рыболов приближается к дому, а на графике это участок, где линия идет вниз при росте времени. Такой участок на графике расположен с \(6\) ч \(30\) мин до \(9\) ч, значит на этом промежутке расстояние от дома уменьшалось.

Если расстояние не меняется, то график горизонтален: значение \(S\) одно и то же при изменении времени. По рисунку горизонтальные отрезки идут с \(2\) ч до \(3\) ч \(30\) мин и с \(4\) ч \(30\) мин до \(6\) ч \(30\) мин, значит на этих промежутках рыболов находился на постоянном расстоянии от дома (не приближался и не удалялся).

г) «Последние два часа» — это промежуток длиной \(2\) часа перед конечным моментом на графике (перед временем \(9\) ч), то есть от \(7\) ч до \(9\) ч. Чтобы найти, сколько он прошел за это время, нужно взять разность расстояний от дома в начале и в конце этого промежутка, потому что на данном участке он возвращается, и пройденный путь по направлению к дому равен уменьшению расстояния \(S\).

По графику за эти \(2\) часа расстояние от дома уменьшилось на \(9{,}5\) км, следовательно, за последние \(2\) часа рыболов прошел \(9{,}5\) км. Это соответствует смыслу: на убывающем участке графика величина пройденного пути за выбранный промежуток равна модулю изменения расстояния до дома на этом промежутке.

д) Скорость на отдельном промежутке движения находим как отношение пройденного пути ко времени: \(v=\frac{s}{t}\). За первый час по графику видно, что рыболов прошел \(4{,}5\) км, значит его скорость на этом часе равна \(v=\frac{4{,}5}{1}=4{,}5\) км/ч.

Аналогично за последний час по графику получается, что он прошел \(4{,}5\) км за \(1\) час, поэтому скорость на последнем часе такая же: \(v=\frac{4{,}5}{1}=4{,}5\) км/ч. Здесь важно, что речь именно о последнем часе движения по графику: сравниваются значения расстояния в начале и конце этого часового интервала, и разность дает путь за час.

Также по графику дано сравнение в промежутке от \(4\) ч до \(4{,}5\) ч: в момент \(4\) ч рыболов был в \(11\) км от дома, то есть \(S(4)=11\), а в момент \(4{,}5\) ч — в \(12\) км от дома, то есть \(S(4{,}5)=12\). Значит за \(30\) минут (это \(0{,}5\) часа) расстояние увеличилось на \(1\) км, то есть за это время он прошел \(1\) км, и скорость равна \(v=\frac{1}{0{,}5}=2\) км/ч.