ГДЗ по Математике 6 Класс Часть 2 Номер 556 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

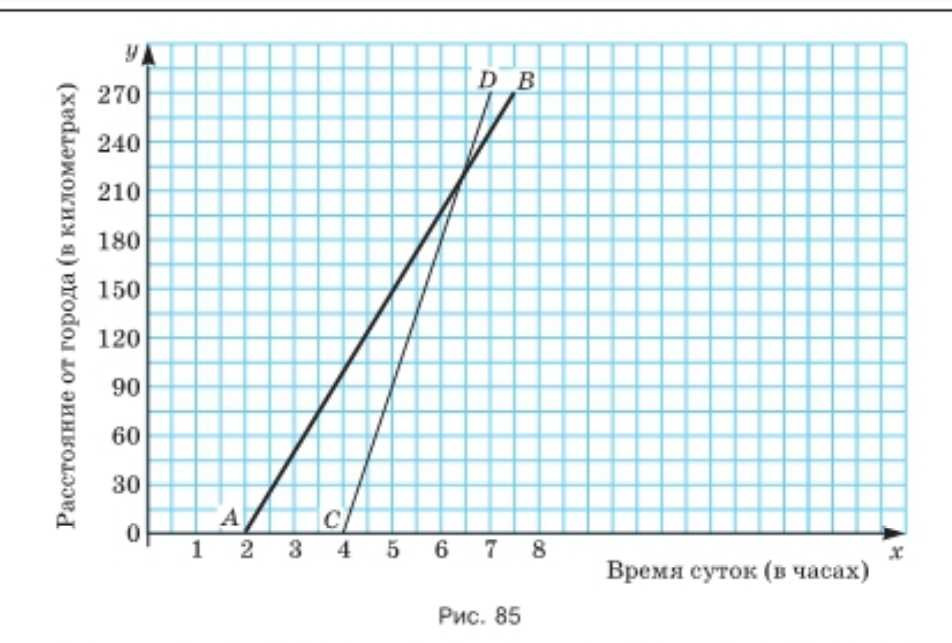
На рисунке 85 изображены графики движения двух автомобилей: грузового (график AB) и легкового (график CD). Определите, пользуясь графиком:
а) в какое время вышли автомобили из города;
б) на каком расстоянии от города был легковой автомобиль в 4 ч 30 мин; в 7 ч;
в) на каком расстоянии от города был грузовой автомобиль в 4 ч; в 6 ч 30 мин;
г) в какое время грузовой автомобиль находился в 135 км от города; в 210 км от города;
д) в какое время легковой автомобиль находился в 135 км от города; в 225 км от города;
е) в какое время и на каком расстоянии от города легковой автомобиль догнал грузовой автомобиль;
ж) какой автомобиль шёл с постоянной скоростью;
з) какова была скорость грузового автомобиля между 5 ч и 6 ч; между 6 ч и 7 ч;
и) на каком расстоянии друг от друга были автомобили в 5 ч; в 7 ч.

а) Грузовой автомобиль вышел из города в 2 ч; легковой автомобиль вышел из города в 4 ч.

б) В 4 ч 30 мин легковой автомобиль был в 45 км от города; в 7 ч он был в 270 км от города.

в) В 4 ч грузовой автомобиль был в 100 км от города; в 6 ч 30 мин он был в 220 км от города.

г) В 4 ч 45 мин грузовой автомобиль был 135 км от города; в 6 ч 15 мин он был в 210 км от города.

д) В 5 ч 30 мин легковой автомобиль был в 135 км от города; в 6 ч 30 мин он был в 220 км от города.

е) Легковой автомобиль в 6 ч 30 мин на расстоянии 220 км от города догнал грузовой автомобиль.

ж) Оба автомобиля шли с постоянной скоростью.

3) Между 5 ч и 6 ч грузовой автомобиль шел со скоростью: \(195 — 150 = 45\) (км/ч).

Между 6 ч и 7 ч грузовой автомобиль шел со скоростью: \(240 — 195 = 45\) (км/ч).

и) В 5 ч между автомобилями было: \(150 — 90 = 60\) (км).

В 7 ч между автомобилями было: \(270 — 240 = 30\) (км).

а) По графику видно, что грузовой автомобиль начинает движение раньше: его линия расстояния от города стартует в момент 2 ч, значит именно тогда он выехал из города. Это читается по тому, что до 2 ч расстояние равно \(0\), а после 2 ч расстояние начинает увеличиваться.

Легковой автомобиль начинает движение позже: его линия расстояния от города выходит из точки \(0\) в момент 4 ч, значит в 4 ч он выехал из города. До 4 ч расстояние от города у легкового равно \(0\), а после 4 ч оно возрастает.

б) В момент 4 ч 30 мин по графику на линии легкового автомобиля расстояние от города равно 45 км, поэтому фиксируем: в 4 ч 30 мин он был в 45 км от города. Это просто считывание значения ординаты (расстояния) в указанное время.

В 7 ч на той же линии легкового автомобиля расстояние равно 270 км, поэтому: в 7 ч он был в 270 км от города. Эти две точки нужны, чтобы понимать положение легкового в разные моменты времени и затем сравнивать с грузовым.

в) В 4 ч по графику на линии грузового автомобиля расстояние от города равно 100 км, поэтому записываем: в 4 ч грузовой был в 100 км от города. Это означает, что к 4 ч грузовой уже прошёл 100 км после выезда в 2 ч.

В 6 ч 30 мин по графику на линии грузового расстояние равно 220 км, значит: в 6 ч 30 мин он был в 220 км от города. Эта точка важна для последующего вывода о встрече, потому что в то же время легковой также оказывается на расстоянии 220 км.

г) В 4 ч 45 мин расстояние грузового автомобиля по графику равно 135 км, поэтому отмечаем: в 4 ч 45 мин он был в 135 км от города. Это очередное считывание с графика координаты точки на линии грузового.

В 6 ч 15 мин по графику расстояние грузового равно 210 км, значит: в 6 ч 15 мин он был в 210 км от города. Эти значения показывают, как равномерно растёт расстояние и подтверждают постоянство скорости.

д) В 5 ч 30 мин по графику на линии легкового расстояние равно 135 км, значит: в 5 ч 30 мин легковой был в 135 км от города. Это показывает, что после выезда в 4 ч легковой быстро наращивает расстояние.

В 6 ч 30 мин по графику расстояние легкового равно 220 км, поэтому: в 6 ч 30 мин он был в 220 км от города. Дальше именно это значение сравнивают с положением грузового в тот же момент времени.

е) В 6 ч 30 мин обе линии (легкового и грузового) на графике проходят через одну и ту же точку по расстоянию 220 км, то есть в один и тот же момент у них одинаковое расстояние от города. Равенство расстояний в один момент означает, что автомобили находятся в одном месте на дороге.

Следовательно, в 6 ч 30 мин на расстоянии 220 км от города легковой догнал грузовой. Смысл «догнал» здесь в том, что легковой выехал позже, но к 6 ч 30 мин сравнялся по положению с грузовым и дальше мог бы оказаться впереди.

ж) Линии движения на графике являются прямыми, то есть расстояние увеличивается равномерно с течением времени. Прямая зависимость расстояния от времени означает постоянную скорость, потому что за равные промежутки времени пройденные расстояния одинаковы.

Это подтверждается тем, что наклон каждой линии не меняется на всём рассматриваемом участке пути. Поэтому делается вывод: оба автомобиля шли с постоянной скоростью.

3) Чтобы найти скорость грузового между 5 ч и 6 ч, берём расстояния грузового в эти моменты по графику: в 5 ч это 150 км, в 6 ч это 195 км. За 1 час прирост расстояния равен \(195 — 150 = 45\), значит скорость на этом промежутке \(45\) км/ч.

Аналогично между 6 ч и 7 ч: в 6 ч грузовой был на 195 км, в 7 ч — на 240 км, прирост за 1 час \(240 — 195 = 45\). Получается та же скорость \(45\) км/ч, что согласуется с постоянной скоростью по прямой линии графика.

и) В 5 ч расстояние грузового от города 150 км, а легкового — 90 км, поэтому расстояние между ними равно разности их расстояний от города: \(150 — 90 = 60\) км. Вычитаем именно так, потому что оба едут в одном направлении от одного города, и отставание измеряется разностью пройденных путей.

В 7 ч грузовой находится на 240 км, а легковой — на 270 км, значит расстояние между ними \(270 — 240 = 30\) км. Здесь легковой уже впереди, поэтому берём разность «легковой минус грузовой», получая 30 км.