ГДЗ по Математике 6 Класс Часть 2 Номер 554 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

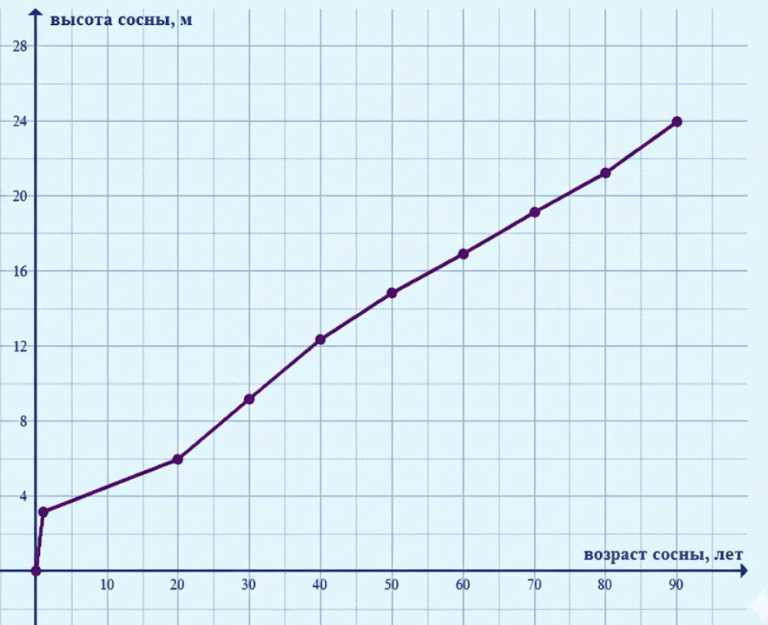
Высота сосны изменялась в зависимости от её возраста следующим образом:

Постройте график зависимости высоты сосны от её возраста. Пользуясь графиком, найдите:
а) высоту сосны в 15 лет; в 35 лет; в 75 лет;
б) возраст сосны, когда её высота была 10 м; 16 м; 20 м;
в) на сколько метров выросла сосна за первые 20 лет; за вторые 20 лет; за третьи 20 лет;
г) на сколько метров выросла сосна за время от 15 до 45 лет.

а) По графику считываем высоты в указанные возраста: в \(15\) лет \(5{,}2\) м; в \(35\) лет \(11\) м; в \(75\) лет \(20{,}2\) м.

б) По графику находим соответствующие возраста для данных высот: при \(10\) м — \(32\) года; при \(16\) м — \(55\) лет; при \(20\) м — \(74\) года.

в) Прирост за каждые \(20\) лет равен разности высот на концах промежутка: за первые \(20\) лет \(6\) м; за вторые \(20\) лет \(12{,}4-6=6{,}4\) м; за третьи \(20\) лет \(17-12{,}4=4{,}6\) м.

г) Прирост с \(15\) до \(45\) лет равен разности высот: \(13{,}2-5{,}2=8\) м.

а) На графике по горизонтальной оси отложен возраст сосны (в годах), а по вертикальной — высота (в метрах). Чтобы найти высоту в заданном возрасте, нужно на оси возраста найти нужное число лет, подняться до точки графика и затем по горизонтали «считать» высоту по шкале слева.

Для возраста \(15\) лет точка графика лежит немного выше уровня \(5\) м и соответствует отметке \(5{,}2\) м, значит в \(15\) лет высота была \(5{,}2\) м. Для возраста \(35\) лет точка расположена на уровне \(11\) м, значит в \(35\) лет высота была \(11\) м. Для возраста \(75\) лет точка находится чуть выше \(20\) м и соответствует \(20{,}2\) м, значит в \(75\) лет высота была \(20{,}2\) м.

б) Здесь наоборот: даны высоты, и нужно определить возраст. Для этого на вертикальной оси находим указанную высоту, проводим мысленно горизонтальную линию до пересечения с графиком и затем опускаемся на ось возраста, чтобы считать количество лет.

При высоте \(10\) м горизонталь пересекает график между \(30\) и \(40\) годами; по отмеченной точке видно, что это \(32\) года, значит в \(32\) года высота была \(10\) м. При высоте \(16\) м пересечение получается между \(50\) и \(60\) годами; по точке графика считываем \(55\) лет, значит в \(55\) лет высота была \(16\) м. При высоте \(20\) м пересечение приходится между \(70\) и \(80\) годами; по графику это \(74\) года, значит в \(74\) года высота была \(20\) м.

в) «За первые (вторые, третьи) 20 лет» означает прирост высоты на каждом промежутке длиной \(20\) лет: \(0\)–\(20\), \(20\)–\(40\), \(40\)–\(60\). Прирост на таком промежутке равен разности высот в конце и в начале этого промежутка: \( \text{прирост} = \text{высота в конце} — \text{высота в начале} \).

По графику: к \(20\) годам высота равна \(6\) м, а в начале (в \(0\) лет) берется \(0\) м, поэтому за первые \(20\) лет прирост \(6\) м. К \(40\) годам высота равна \(12{,}4\) м, а к \(20\) годам — \(6\) м, значит за вторые \(20\) лет прирост \(12{,}4-6=6{,}4\) м. К \(60\) годам высота равна \(17\) м, а к \(40\) годам — \(12{,}4\) м, значит за третьи \(20\) лет прирост \(17-12{,}4=4{,}6\) м.

г) Нужно найти, насколько изменилась высота между двумя возрастами, поэтому берём высоты в эти моменты времени по графику и находим разность «позже минус раньше». Это стандартный способ найти прирост величины по графику: \( \text{прирост} = h_2 — h_1 \).

С графика: в \(15\) лет высота \(5{,}2\) м, а в \(45\) лет высота \(13{,}2\) м (точка находится между \(40\) и \(50\) годами на уровне \(13{,}2\) м). Тогда прирост равен \(13{,}2-5{,}2=8\) м, то есть за период с \(15\) до \(45\) лет сосна выросла на \(8\) м.