ГДЗ по Математике 6 Класс Часть 2 Номер 552 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

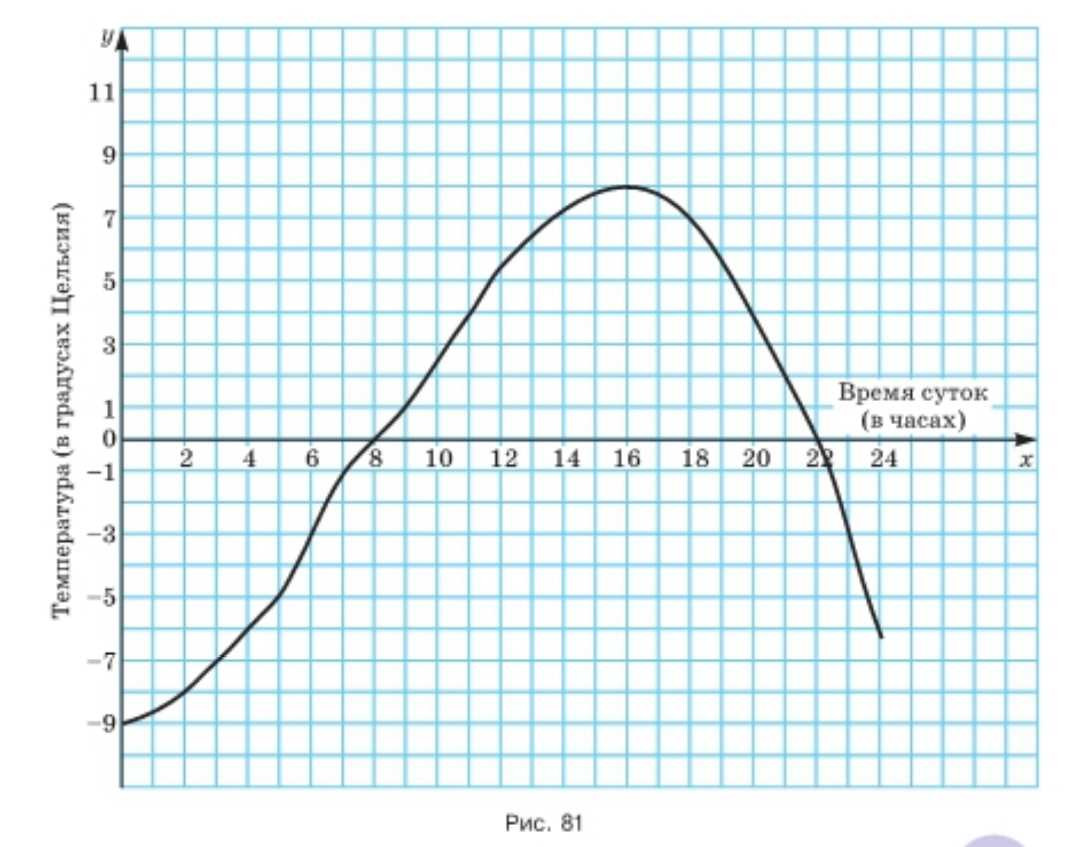
На рисунке 81 изображён график изменения температуры воздуха в течение суток. Ответьте на следующие вопросы:
а) Чему равнялась температура воздуха в 3 ч; в 12 ч?
б) В какие часы температура воздуха была отрицательной?
в) В какие часы температура воздуха была положительной?
г) Когда температура воздуха равнялась нулю; \(2^\circ\) С; \(-6^\circ\) С?
д) На сколько градусов изменилась температура с 2 ч до 13 ч; с 18 ч до 24 ч?

а) В 3 ч \(t=-7^\circ C\), в 12 ч \(t=5{,}5^\circ C\).

б) Температура воздуха была отрицательной с 0 ч до 8 ч и с 22 ч до 24 ч.

в) Температура воздуха была положительной с 8 ч до 22 ч.

г) В 8 ч и 22 ч \(t=0^\circ C\); в 9,5 ч и 21 ч \(t=2^\circ C\); в 4 ч и 24 ч \(t=-6^\circ C\).

д) В 2 ч \(t=-8^\circ C\), в 13 ч \(t=6{,}5^\circ C\), значит, температура повысилась на: \(6{,}5-(-8)=6{,}5+8=14{,}5^\circ C\).

В 18 ч \(t=7^\circ C\), в 24 ч \(t=-6^\circ C\), значит, температура понизилась на: \(7-(-6)=13^\circ C\).

а) Даны два момента времени и соответствующие им значения температуры: в 3 ч температура была \(t=-7^\circ C\), а в 12 ч температура была \(t=5{,}5^\circ C\). Здесь требуется просто корректно считать значения с графика (или из условия) и записать их, соблюдая знак: при отрицательной температуре ставим минус, при положительной — пишем число без минуса.

Запись оформляется как пара «время — температура»: \(3\) ч соответствует \(t=-7^\circ C\), а \(12\) ч соответствует \(t=5{,}5^\circ C\). Эти числа дальше могут использоваться для сравнения или вычисления изменения температуры, но в этом пункте фиксируются именно сами значения.

б) Нужно указать промежутки времени, когда температура была ниже нуля, то есть \(t<0^\circ C\). По данным видно, что линия температуры находится ниже отметки \(0^\circ C\) в начале суток до момента пересечения нуля и снова уходит в отрицательные значения ближе к концу суток. Поэтому отрицательная температура наблюдалась с 0 ч до 8 ч и с 22 ч до 24 ч. Границы \(8\) ч и \(22\) ч являются моментами, когда \(t=0^\circ C\), поэтому внутри указанных промежутков температура отрицательная, а в самих точках границы равна нулю. в) Нужно указать промежуток, когда температура была выше нуля, то есть \(t>0^\circ C\). По данным нулевая отметка достигается в 8 ч и затем температура поднимается выше нуля и держится положительной до следующего возвращения к нулю.

Следовательно, положительная температура была с 8 ч до 22 ч. Внутри этого промежутка \(t>0^\circ C\), а в граничные моменты \(8\) ч и \(22\) ч температура равна нулю, поэтому эти моменты выделяются отдельно в следующем пункте.

г) Здесь нужно перечислить конкретные моменты времени, когда температура принимала заданные значения. Сначала отмечаются моменты пересечения уровня \(0^\circ C\): по данным это происходит в 8 ч и 22 ч, поэтому в эти моменты \(t=0^\circ C\).

Далее фиксируются моменты, когда температура равнялась \(2^\circ C\): это 9,5 ч и 21 ч, то есть в \(9{,}5\) ч и в \(21\) ч имеем \(t=2^\circ C\). Также отмечаются моменты, когда температура равнялась \(-6^\circ C\): это 4 ч и 24 ч, значит в 4 ч и 24 ч \(t=-6^\circ C\).

д) Сначала находится, на сколько изменилась температура от 2 ч до 13 ч. В 2 ч было \(t=-8^\circ C\), в 13 ч стало \(t=6{,}5^\circ C\). Повышение температуры — это разность «конечная минус начальная», поэтому считаем \(6{,}5-(-8)\).

Так как вычитание отрицательного числа превращается в сложение, получаем \(6{,}5-(-8)=6{,}5+8=14{,}5^\circ C\). Затем определяется, на сколько понизилась температура от 18 ч до 24 ч: в 18 ч \(t=7^\circ C\), а в 24 ч \(t=-6^\circ C\), уменьшение по модулю находим разностью \(7-(-6)\), откуда \(7-(-6)=13^\circ C\).