
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 54 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
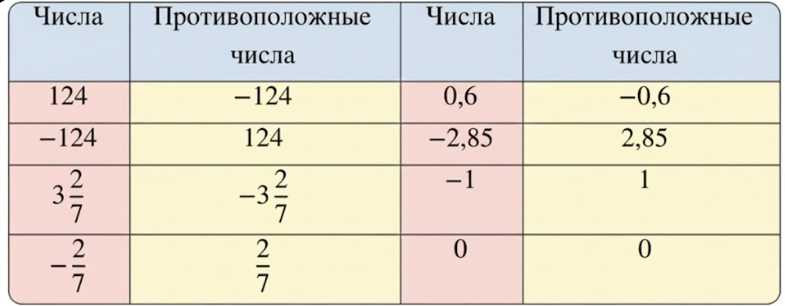
Какие числа противоположны числам:
124; −124; \(3\frac{3}{7};\ -\frac{2}{7};\ 0,6;\ -2,85;\ -1;\ 0\)?
Числа и их противоположные значения:
\(124\) и \(-124\) являются противоположными числами. Их сумма равна \(0\), поскольку \(124 + (-124) = 0\). Противоположные числа имеют одинаковую абсолютную величину, но противоположные знаки.
\(-124\) и \(124\) также являются противоположными числами. Их сумма также равна \(0\), так как \(-124 + 124 = 0\).
\(\frac{2}{7}\) и \(-\frac{2}{7}\) — это противоположные числа. Их разность равна \(\frac{4}{7}\), поскольку \(\frac{2}{7} — (-\frac{2}{7}) = \frac{2}{7} + \frac{2}{7} = \frac{4}{7}\).
\(\frac{2}{7}\) и \(0\) — это противоположные числа. Их сумма равна \(\frac{2}{7}\), так как \(\frac{2}{7} + 0 = \frac{2}{7}\).
\(-\frac{3}{2}\) и \(\frac{3}{2}\) — это противоположные числа. Их сумма равна \(0\), поскольку \(-\frac{3}{2} + \frac{3}{2} = 0\).
Числа и их противоположные значения:
\(124\) и \(-124\) являются противоположными числами. Их сумма равна \(0\), поскольку \(124 + (-124) = 0\). Противоположные числа имеют одинаковую абсолютную величину, но противоположные знаки.
\(-124\) и \(124\) также являются противоположными числами. Их сумма также равна \(0\), так как \(-124 + 124 = 0\).
\(\frac{2}{7}\) и \(-\frac{2}{7}\) — это противоположные числа. Их разность равна \(\frac{4}{7}\), поскольку \(\frac{2}{7} — (-\frac{2}{7}) = \frac{2}{7} + \frac{2}{7} = \frac{4}{7}\).
\(\frac{2}{7}\) и \(0\) — это противоположные числа. Их сумма равна \(\frac{2}{7}\), так как \(\frac{2}{7} + 0 = \frac{2}{7}\).
\(-\frac{3}{2}\) и \(\frac{3}{2}\) — это противоположные числа. Их сумма равна \(0\), поскольку \(-\frac{3}{2} + \frac{3}{2} = 0\).
Таким образом, противоположные числа имеют одинаковую абсолютную величину, но противоположные знаки, и их сумма равна \(0\).






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!