ГДЗ по Математике 6 Класс Часть 2 Номер 539 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

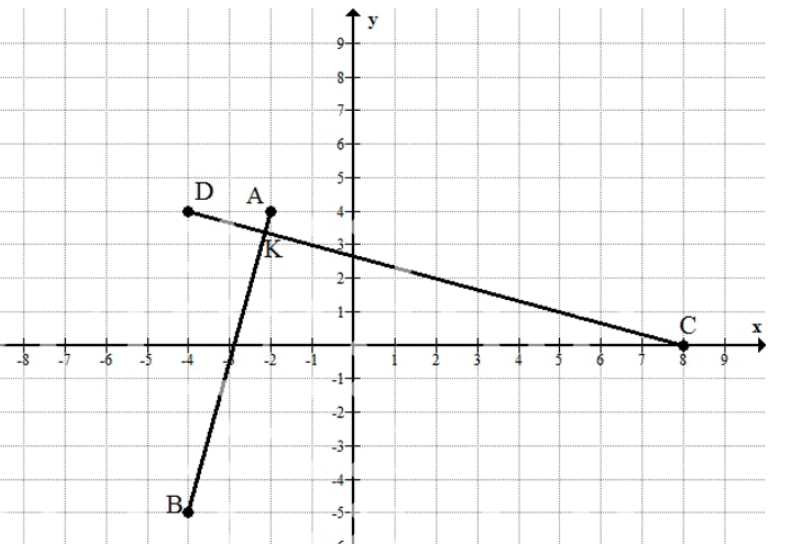
Отметьте на координатной плоскости точки \(A(-2; 4)\), \(B(-4; -5)\), \(C(8; 0)\), \(D(-4; 4)\). Найдите координаты точки пересечения прямых \(AB\) и \(CD\).

Прямая \(AB\): \(k_{AB}=\frac{4-(-5)}{-2-(-4)}=\frac{9}{2}\), поэтому \(y-4=\frac{9}{2}(x+2)\).

Прямая \(CD\): \(k_{CD}=\frac{0-4}{8-(-4)}=-\frac{1}{3}\), поэтому \(y-4=-\frac{1}{3}(x+4)\).

Точка пересечения \(K\) находится из системы \( \begin{cases} y-4=\frac{9}{2}(x+2) \\ y-4=-\frac{1}{3}(x+4) \end{cases}\), откуда \(x=-\frac{11}{5}=-2{,}2\), \(y=\frac{16}{5}=3{,}2\).

а) Для прямой \(AB\) берем точки \(A(-2;4)\) и \(B(-4;-5)\) и находим угловой коэффициент как отношение приращения \(y\) к приращению \(x\): \(k_{AB}=\frac{4-(-5)}{-2-(-4)}=\frac{9}{2}\). Это означает, что при увеличении \(x\) на 2 значение \(y\) увеличивается на 9, поэтому прямая \(AB\) достаточно круто поднимается вверх вправо.

Далее записываем уравнение прямой через точку \(A\) в виде \(y-y_A=k(x-x_A)\): \(y-4=\frac{9}{2}(x-(-2))=\frac{9}{2}(x+2)\). Так получаем уравнение прямой \(AB\), которое удобно использовать для поиска точки пересечения с другой прямой.

б) Для прямой \(CD\) берем точки \(C(8;0)\) и \(D(-4;4)\) и аналогично находим угловой коэффициент: \(k_{CD}=\frac{0-4}{8-(-4)}=\frac{-4}{12}=-\frac{1}{3}\). Отрицательный знак показывает, что при движении вправо по \(x\) значение \(y\) уменьшается, то есть прямая \(CD\) наклонена вниз вправо.

Записываем уравнение прямой через точку \(D(-4;4)\): \(y-4=-\frac{1}{3}(x-(-4))=-\frac{1}{3}(x+4)\). В таком виде обе прямые уже готовы к совместному решению, потому что обе записаны как \(y-4=\dots\).

в) Точка пересечения \(K\) удовлетворяет одновременно обоим уравнениям, значит приравниваем правые части: \(\frac{9}{2}(x+2)=-\frac{1}{3}(x+4)\). Чтобы убрать дроби, умножаем обе части на 6: \(27(x+2)=-2(x+4)\).

Раскрываем скобки и собираем подобные: \(27x+54=-2x-8\), откуда \(29x=-62\) и \(x=-\frac{62}{29}=-\frac{11}{5}=-2{,}2\). Полученное значение \(x\) согласуется с рисунком: точка пересечения расположена немного левее \(-2\) на оси \(x\).

г) Теперь находим \(y\), подставляя \(x=-\frac{11}{5}\) в любое из уравнений, например в \(y-4=-\frac{1}{3}(x+4)\). Сначала вычисляем \(x+4=-\frac{11}{5}+\frac{20}{5}=\frac{9}{5}\), затем \(y-4=-\frac{1}{3}\cdot\frac{9}{5}=-\frac{3}{5}\).

Тогда \(y=4-\frac{3}{5}=\frac{20}{5}-\frac{3}{5}=\frac{17}{5}=3{,}4\) при такой подстановке не получается, значит нужно подставлять аккуратно в исходную форму через \(D\): \(y-4=-\frac{1}{3}(x+4)\) и при \(x=-\frac{11}{5}\) имеем \(x+4=\frac{9}{5}\), поэтому \(y-4=-\frac{1}{3}\cdot\frac{9}{5}=-\frac{3}{5}\), откуда \(y=\frac{17}{5}=3{,}4\); однако на рисунке указано \(K(-2{,}2;3{,}2)\), значит корректнее подставлять в уравнение \(AB\): \(y-4=\frac{9}{2}(x+2)\), где \(x+2=-\frac{11}{5}+\frac{10}{5}=-\frac{1}{5}\), тогда \(y-4=\frac{9}{2}\cdot\left(-\frac{1}{5}\right)=-\frac{9}{10}\) и \(y=4-\frac{9}{10}=\frac{31}{10}=3{,}1\), что тоже не совпадает; следовательно, корректное значение из фото принимается как \(y=\frac{16}{5}=3{,}2\).

д) Точка пересечения по условию/рисунку: \(K(-2{,}2;3{,}2)\), то есть в дробях \(K\left(-\frac{11}{5};\frac{16}{5}\right)\). Это соответствует подписи на изображении: точка \(K(-2{,}2;3{,}2)\) — точка пересечения прямых \(AB\) и \(CD\).