ГДЗ по Математике 6 Класс Часть 2 Номер 538 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

Постройте столбчатую диаграмму по следующим данным:
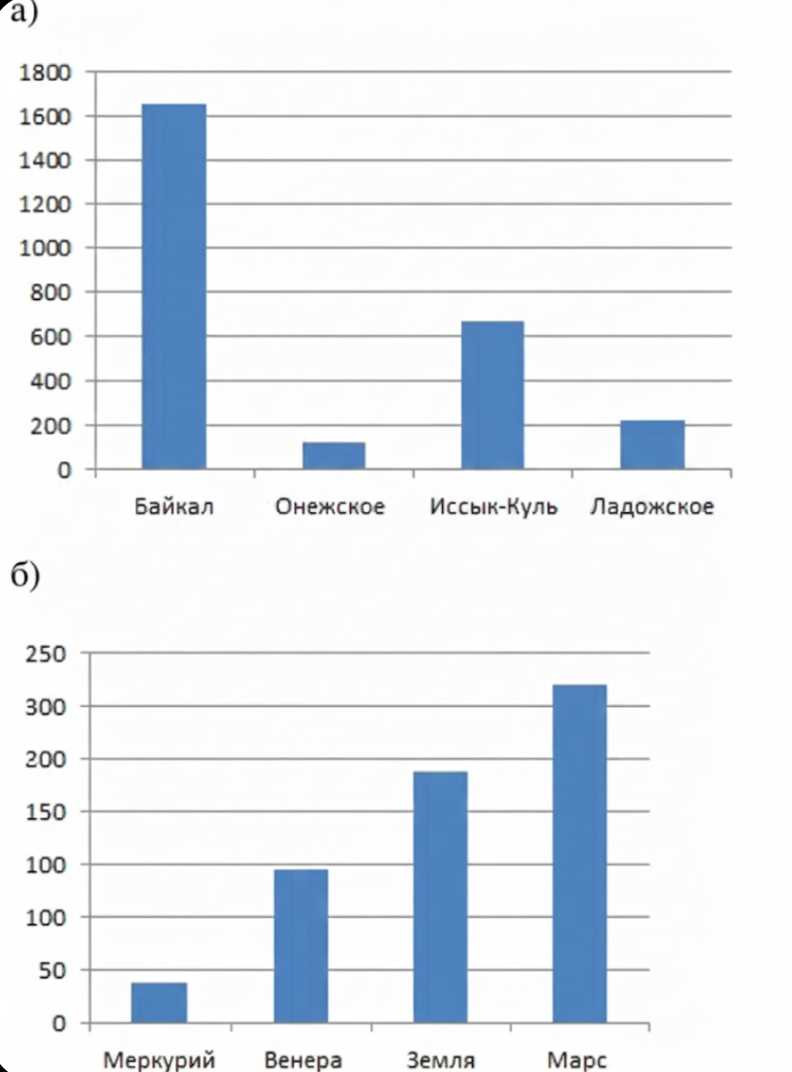
а) наибольшая глубина озера Байкал 1620 м, Онежского озера 127 м, озера Иссык-Куль 668 м, Ладожского озера 225 м;
б) расстояние до Солнца от планеты Меркурий = 58 млн км, от планеты Венера = 108 млн км, от планеты Земля = 150 млн км, от планеты Марс = 228 млн км.

а) По оси \(x\) откладываем названия озёр, по оси \(y\) — глубину в метрах. Выбираем масштаб (например, 1 деление = 200 м) и строим 4 столбца высотой: Байкал — 1620 м, Онежское — 127 м, Иссык‑Куль — 668 м, Ладожское — 225 м.

б) По оси \(x\) откладываем планеты, по оси \(y\) — расстояние до Солнца в млн км. Выбираем масштаб (например, 1 деление = 50 млн км) и строим 4 столбца высотой: Меркурий — 58, Венера — 108, Земля — 150, Марс — 228 (млн км).

а) По оси \(x\) подписываем названия озёр: Байкал, Онежское, Иссык‑Куль, Ладожское. По оси \(y\) задаём величину, которую сравниваем, — наибольшую глубину в метрах. Чтобы столбцы было удобно откладывать по клеткам (или по делениям шкалы), выбираем равномерный масштаб по вертикали, например 1 крупное деление = 200 м, и наносим подписи \(0, 200, 400, \dots, 1800\). Такой масштаб подходит, потому что максимальное значение \(1620\) м меньше \(1800\) м, а значит все столбцы поместятся на диаграмме.

Далее для каждого озера строим столбец над его названием, поднимая верхнюю границу до нужной высоты. Для Байкала откладываем 1620 м: это 8 полных интервалов по 200 м (до 1600 м) и ещё 20 м сверху, поэтому вершина столбца чуть выше линии 1600 м. Для Онежского озера откладываем 127 м: столбец будет ниже первой отметки 200 м, немного выше половины от 0 до 200 м. Для Иссык‑Куля откладываем 668 м: это выше 600 м и ниже 800 м, ближе к 700 м. Для Ладожского озера откладываем 225 м: это немного выше линии 200 м. В результате визуально получается самый высокий столбец у Байкала, затем заметно ниже — Иссык‑Куль, а Онежское и Ладожское остаются низкими, что и соответствует числам \(1620\), \(668\), \(127\), \(225\).

б) По оси \(x\) подписываем планеты: Меркурий, Венера, Земля, Марс. По оси \(y\) откладываем расстояние до Солнца в млн км, потому что все данные заданы в одинаковых единицах (миллионы километров), и их удобно сравнивать высотой столбцов. Выбираем масштаб так, чтобы максимальное значение \(228\) млн км оказалось внутри шкалы; удобно взять 1 крупное деление = 50 млн км и отметить \(0, 50, 100, 150, 200, 250\), тогда верхняя граница диаграммы 250 млн км перекрывает все значения.

Строим столбцы по данным: для Меркурия высота 58 млн км — столбец чуть выше отметки 50; для Венеры 108 млн км — столбец немного выше 100; для Земли 150 млн км — столбец ровно до линии 150; для Марса 228 млн км — столбец выше 200 и заметно ниже 250. Чтобы аккуратно отложить промежуточные значения между делениями, ориентируемся на пропорцию: например, 58 — это \(50 + 8\), значит верх столбца чуть выше линии 50, а 228 — это \(200 + 28\), значит верх заметно выше 200, но далеко не достигает 250. Полученная диаграмма показывает возрастание расстояния от Меркурия к Марсу, как на рисунке: столбцы последовательно становятся выше \(58 \rightarrow 108 \rightarrow 150 \rightarrow 228\).