ГДЗ по Математике 6 Класс Часть 2 Номер 536 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

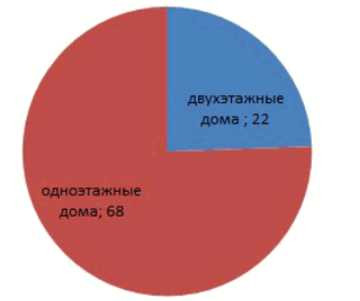
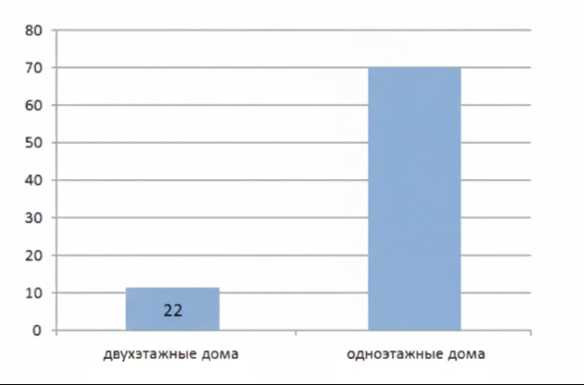
В селе 22 двухэтажных дома, а остальные 68 — одноэтажные. Постройте круговую и столбчатую диаграммы (один дом — 2 мм).

1) Всего домов в селе: \(22+68=90\).

2) Угол сектора для двухэтажных домов: \(\frac{22}{90}\cdot 360=\frac{11}{45}\cdot 360=\frac{11}{5}\cdot 40=11\cdot 8=88^\circ\).

1) Всего домов в селе: \(22+68=90\). Здесь складываем количество двухэтажных домов и количество одноэтажных домов, потому что вместе они составляют все дома в селе. Это нужно, чтобы дальше можно было находить долю двухэтажных домов от общего числа.

Полученное общее число \(90\) — это целое, которому соответствует полный круг диаграммы. То есть именно от \(90\) домов мы будем брать нужную часть для сектора, соответствующего двухэтажным домам.

2) Двухэтажные дома в селе соответствуют сектору круга: \(\frac{22}{90}\cdot 360=\frac{11}{45}\cdot 360=\frac{11}{5}\cdot 40=11\cdot 8=88^\circ\). Сначала находим долю двухэтажных домов среди всех домов: это \(\frac{22}{90}\), потому что двухэтажных \(22\), а всего \(90\). Эта дробь показывает, какую часть от полного круга должен занимать сектор.

Так как полный круг равен \(360^\circ\), то угловая величина сектора находится умножением доли на \(360^\circ\): \(\frac{22}{90}\cdot 360\). Для удобства сокращаем дробь \(\frac{22}{90}\) на \(2\) и получаем \(\frac{11}{45}\), после чего считаем: \(\frac{11}{45}\cdot 360\). Затем упрощаем вычисления, заменяя \(360\) на \(9\cdot 40\), чтобы сократить с \(45\): \(\frac{11}{45}\cdot 360=\frac{11}{45}\cdot 9\cdot 40=\frac{11}{5}\cdot 40\), и получаем \(88^\circ\).