ГДЗ по Математике 6 Класс Часть 2 Номер 534 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

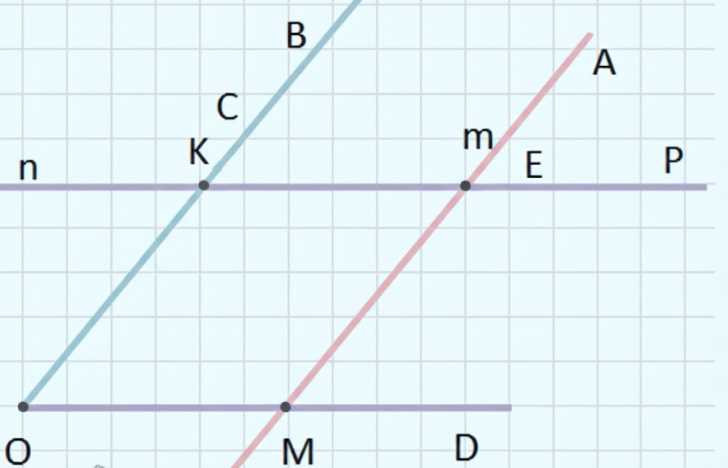
Постройте угол \(COD\), равный \(50^\circ\). Через точку \(M\), лежащую на стороне \(OD\), проведите прямую \(m\), параллельную стороне \(OC\), а через точку \(K\), лежащую на стороне \(OC\), проведите прямую \(n\), параллельную стороне \(OD\). Измерьте транспортиром углы, образовавшиеся при пересечении прямых \(m\) и \(n\).

Так как угол \(COD=50^\circ\), то угол \(OME=180^\circ-50^\circ=130^\circ\).

Значит, угол \(AEP=50^\circ\), угол \(AEK=130^\circ\), угол \(PEM=130^\circ\), угол \(MEK=50^\circ\).

На рисунке угол \(COD\) задан равным \(50^\circ\). Лучи \(OC\) и \(OD\) образуют острый угол при точке \(O\). При этом угол \(OME\) является смежным с углом, равным \(50^\circ\), потому что в точке \(M\) одна сторона угла \(OME\) лежит на продолжении прямой, образующей угол \(COD\), а другая сторона — на пересекающей её прямой, и эти два угла составляют развернутый угол.

Так как смежные углы в сумме дают \(180^\circ\), то величина угла \(OME\) находится вычитанием: \(OME=180^\circ-50^\circ=130^\circ\). Это означает, что в точке \(M\) при пересечении прямых один из углов острый \(50^\circ\), а смежный с ним — тупой \(130^\circ\), и далее при переносе к другим точкам пересечения сохраняются те же значения (острый \(50^\circ\) и тупой \(130^\circ\)).

Угол \(AEP\) равен \(50^\circ\), потому что в точке \(E\) наклонная прямая (проходящая через \(A\)) пересекает горизонтальную прямую (на которой лежит \(P\)), и угол \(AEP\) занимает то же положение относительно пересекающихся прямых, что и угол \(COD\): это соответствующий острый угол при параллельных наклонных и общей горизонтали, поэтому его величина сохраняется и равна \(50^\circ\).

Угол \(AEK\) равен \(130^\circ\), так как в точке \(E\) угол \(AEK\) смежен с углом \(AEP\): луч \(EA\) общий, а лучи \(EP\) и \(EK\) лежат на одной прямой в противоположных направлениях. Следовательно, \(AEK=180^\circ-50^\circ=130^\circ\), то есть это тупой угол, дополняющий острый угол \(AEP\) до развернутого.

Угол \(PEM\) равен \(130^\circ\), потому что он вертикален углу \(AEK\) при пересечении тех же двух прямых в точке \(E\): лучи \(EP\) и \(EK\) — противоположные, и лучи \(EM\) и \(EA\) — тоже противоположные на одной наклонной. Вертикальные углы равны, значит \(PEM=AEK=130^\circ\).

Угол \(MEK\) равен \(50^\circ\), так как он вертикален углу \(AEP\) в точке \(E\): стороны угла \(MEK\) образованы лучами \(EM\) и \(EK\), которые являются противоположными соответственно лучам \(EA\) и \(EP\). Поэтому \(MEK=AEP=50^\circ\), и этот угол является острым, как и угол \(AEP\).