
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 533 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
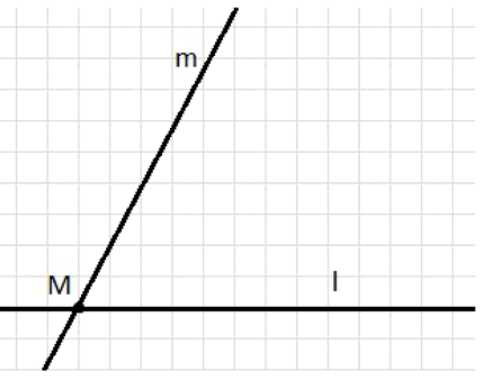
Отметьте точку \(M\) и проведите через неё две прямые — \(m\) и \(l\) — так, чтобы они образовали угол, равный \(62^\circ\).
Отметьте точку \(M\) и проведите через неё две прямые — \(m\) и \(l\) — так, чтобы они образовали угол, равный \(62^\circ\).
а) Поставьте на листе точку \(M\) — это будет вершина нужного угла, поэтому обе прямые обязательно должны проходить через неё. Чтобы конструкция была точной, отметку делайте чётко (карандашом) и сразу подпишите \(M\), чтобы не перепутать вершину при измерении угла транспортиром.
Проведите через точку \(M\) первую прямую и обозначьте её \(m\). Для этого приложите линейку так, чтобы её край проходил через \(M\), и проведите линию в обе стороны, получив прямую. Эта прямая будет одной стороной угла, поэтому дальше все измерения угла удобно выполнять, считая \(m\) исходным направлением.
Приложите транспортир центром (отверстием или отметкой центра) точно к точке \(M\), а его нулевую линию совместите с прямой \(m\) (то есть чтобы основание транспортира лежало вдоль \(m\)). После совмещения выберите нужную шкалу (ту, где отсчёт начинается от \(0^\circ\) именно на стороне совпадения с \(m\)) и найдите отметку \(62^\circ\). Поставьте небольшую точку на луче, соответствующем направлению \(62^\circ\), чтобы зафиксировать вторую сторону угла.
Уберите транспортир и проведите через точки \(M\) и отмеченную точку прямую — это и будет прямая \(l\). Проводите линию аккуратно по линейке в обе стороны, чтобы получилась именно прямая, а не короткий луч. В результате прямые \(m\) и \(l\) пересекаются в точке \(M\) и образуют угол заданной величины, то есть \(\angle(m,l)=62^\circ\) (берём меньший угол между прямыми).
Если при проверке получается другой угол, чаще всего причина в выборе неверной шкалы транспортира или в том, что нулевая линия была совмещена не с \(m\), а с её продолжением в противоположную сторону. В таком случае снова совместите транспортир с \(m\), отложите ровно \(62^\circ\) от нужного направления и заново проведите \(l\), чтобы меньший угол между \(m\) и \(l\) был равен \(62^\circ\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!