
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 531 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
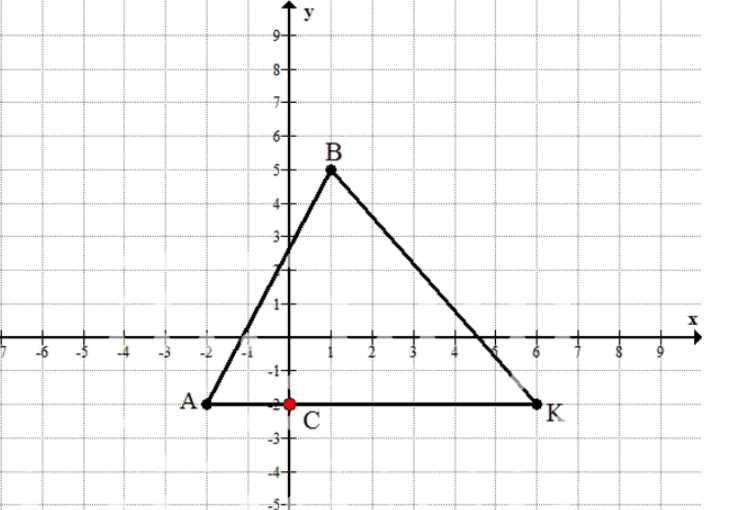
Постройте треугольник \(ABK\) по координатам его вершин \(A(-2;\,-2)\), \(B(1;\,5)\), \(K(6;\,-2)\). Найдите координаты точки пересечения стороны \(AK\) с осью ординат.
Сторона \(AK\) проходит через точки \(A(-2;\,-2)\) и \(K(6;\,-2)\), значит это горизонтальная прямая \(y=-2\).
Ось ординат задаётся уравнением \(x=0\). При пересечении получаем точку \(C(0;\,-2)\).
а) Чтобы найти точку пересечения стороны \(AK\) с осью ординат, сначала выпишем координаты концов этой стороны: \(A(-2;\,-2)\) и \(K(6;\,-2)\). У этих двух точек одинаковая ордината: у \(A\) \(y=-2\) и у \(K\) \(y=-2\). Это означает, что отрезок \(AK\) лежит на горизонтальной прямой, параллельной оси \(Ox\).
Раз ордината постоянна и равна \(-2\) для всех точек стороны \(AK\), то уравнение прямой, содержащей сторону \(AK\), имеет вид \(y=-2\). Теперь используем, что ось ординат — это множество всех точек, у которых абсцисса равна нулю, то есть \(x=0\).
Точка пересечения должна одновременно лежать на стороне \(AK\) и на оси ординат, значит её координаты должны удовлетворять сразу двум условиям: \(y=-2\) и \(x=0\). Подставляя \(x=0\) и сохраняя найденную ординату \(-2\), получаем точку пересечения \(C(0;\,-2)\), что совпадает с изображением на рисунке (красная точка на оси \(Oy\) на уровне \(y=-2\)).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!