
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 529 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
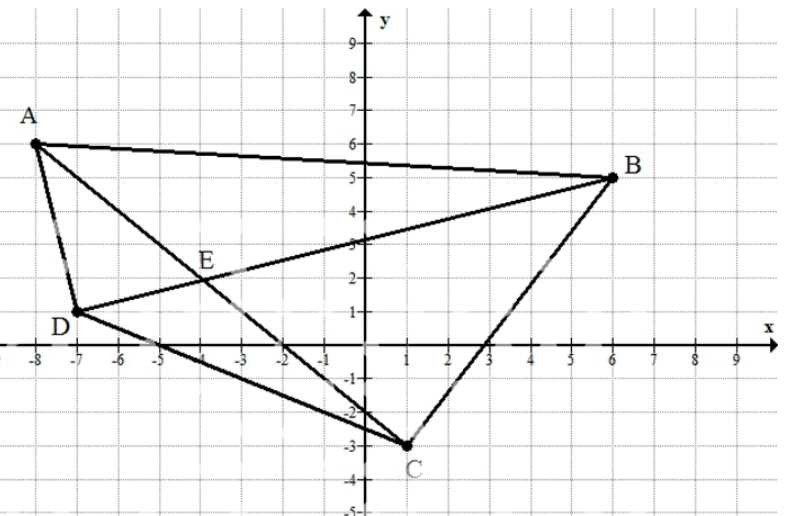
Постройте четырёхугольник \(ABCD\) по координатам его вершин \(A(-8;\,6)\), \(B(6;\,5)\), \(C(1;\,-3)\), \(D(-7;\,1)\). Найдите координаты точки пересечения отрезков \(AC\) и \(BD\).
Пусть точка пересечения диагоналей \(AC\) и \(BD\) имеет координаты \((x;y)\). Удобно задать прямые через параметры: для \(AC\) вектор \(\overrightarrow{AC}=(1-(-8);\,-3-6)=(9;\,-9)\), значит \((x;y)=(-8;6)+t(9;\,-9)\), то есть \(x=-8+9t\), \(y=6-9t\).
Для \(BD\) вектор \(\overrightarrow{BD}=(-7-6;\,1-5)=(-13;\,-4)\), значит \((x;y)=(6;5)+s(-13;\,-4)\), то есть \(x=6-13s\), \(y=5-4s\). В точке пересечения выполняется система \(-8+9t=6-13s\) и \(6-9t=5-4s\); из неё получаем \(t=\frac{23}{51}\).
Подставляем \(t=\frac{23}{51}\) в формулы для \(AC\): \(x=-8+9\cdot\frac{23}{51}=\frac{-67}{17}\), \(y=6-9\cdot\frac{23}{51}=\frac{33}{17}\). Следовательно, точка пересечения отрезков \(AC\) и \(BD\) равна \(\left(\frac{-67}{17};\frac{33}{17}\right)\).
Чтобы построить четырёхугольник \(ABCD\), на координатной плоскости отмечают точки \(A(-8;6)\), \(B(6;5)\), \(C(1;-3)\), \(D(-7;1)\) и соединяют их последовательно отрезками \(AB\), \(BC\), \(CD\), \(DA\). Диагонали этого четырёхугольника — отрезки \(AC\) и \(BD\); требуется найти их точку пересечения как общую точку прямых, содержащих эти отрезки.
Запишем уравнения диагоналей в параметрическом виде. Для \(AC\): направляющий вектор \( \overrightarrow{AC}=(1-(-8);\,-3-6)=(9;\,-9)\), поэтому любая точка на \(AC\) имеет вид \( (x;y)=(-8;6)+t(9;-9)\), то есть \(x=-8+9t\), \(y=6-9t\). Для \(BD\): \( \overrightarrow{BD}=(-7-6;\,1-5)=(-13;\,-4)\), значит \( (x;y)=(6;5)+s(-13;-4)\), то есть \(x=6-13s\), \(y=5-4s\).
В точке пересечения координаты должны совпадать, поэтому решаем систему \( -8+9t=6-13s\) и \( 6-9t=5-4s\). Из второго уравнения получаем \(1-9t=-4s\), откуда \( s=\frac{9t-1}{4}\). Подставляя в первое: \( -8+9t=6-13\cdot\frac{9t-1}{4}\), умножаем на \(4\): \( -32+36t=24-13(9t-1)=24-117t+13\), значит \( -32+36t=37-117t\), откуда \(153t=69\) и \( t=\frac{23}{51}\).
Подставляем \( t=\frac{23}{51}\) в параметры диагонали \(AC\): \(x=-8+9\cdot\frac{23}{51}=-8+\frac{207}{51}=-8+\frac{69}{17}=\frac{-67}{17}\), \(y=6-9\cdot\frac{23}{51}=6-\frac{207}{51}=6-\frac{69}{17}=\frac{33}{17}\). Следовательно, точка пересечения отрезков \(AC\) и \(BD\) имеет координаты \(\left(\frac{-67}{17};\frac{33}{17}\right)\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!