
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 520 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
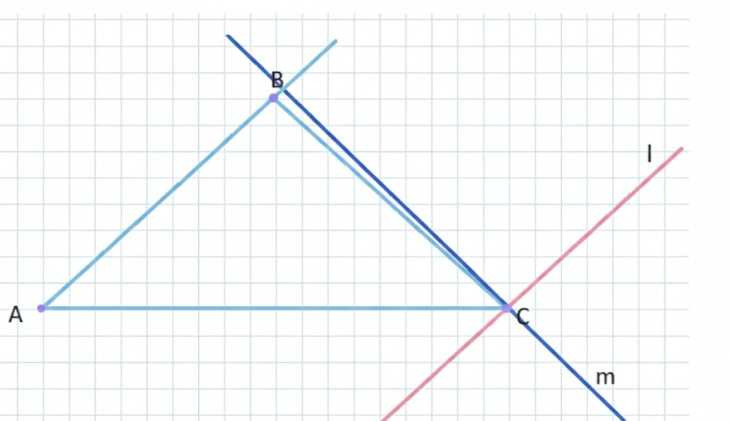
Начертите какой-нибудь треугольник \(ABC\). Через вершину \(C\) проведите прямую \(l\), параллельную стороне \(AB\), и прямую \(m\), перпендикулярную стороне \(AB\).
Проведём через \(C\) прямую \(l\) так, что \(l \parallel AB\), и прямую \(m\) так, что \(m \perp AB\).
Так как \(l \parallel AB\), то угол между \(l\) и \(AB\) равен \(0^\circ\). Поскольку \(m \perp AB\), угол между \(m\) и \(AB\) равен \(90^\circ\).
Следовательно, угол между \(l\) и \(m\) равен \(90^\circ\), то есть \(l \perp m\).
а) Начертим произвольный треугольник \(ABC\): это значит, что точки \(A\), \(B\), \(C\) не лежат на одной прямой, а отрезки \(AB\), \(BC\), \(CA\) образуют треугольник. Важно, что сторона \(AB\) уже задана как конкретная прямая (если продолжить отрезок \(AB\) в обе стороны), относительно которой мы будем строить новые прямые.
Через вершину \(C\) проведём прямую \(l\), параллельную стороне \(AB\), то есть такую, что \(l \parallel AB\). По смыслу параллельности это означает: прямая \(l\) имеет то же направление, что и прямая \(AB\), и при продолжении они не пересекутся. Такое построение всегда возможно и единственно: через точку \(C\), не лежащую на прямой \(AB\), можно провести ровно одну прямую, параллельную \(AB\).
б) Теперь через ту же вершину \(C\) проведём прямую \(m\), перпендикулярную стороне \(AB\), то есть такую, что \(m \perp AB\). Перпендикулярность означает, что при пересечении \(m\) с прямой \(AB\) образуется прямой угол, равный \(90^\circ\).
Это построение также всегда возможно и единственно: через любую точку (в том числе через \(C\)) можно провести ровно одну прямую, перпендикулярную данной прямой \(AB\). Поэтому прямая \(m\) однозначно определяется условием \(m \perp AB\), так же как прямая \(l\) однозначно определяется условием \(l \parallel AB\).
в) Рассмотрим углы, которые образуют прямые \(l\) и \(m\) с прямой \(AB\). Так как \(l \parallel AB\), то направление \(l\) совпадает с направлением \(AB\), а значит угол между \(l\) и \(AB\) равен \(0^\circ\) (прямые «идут одинаково», без поворота относительно друг друга). Одновременно по построению \(m \perp AB\), то есть угол между \(m\) и \(AB\) равен \(90^\circ\).
Чтобы перейти к углу между \(l\) и \(m\), используем идею «поворота» относительно одной и той же прямой \(AB\): если от направления \(AB\) повернуть на \(0^\circ\), получим направление \(l\), а если от направления \(AB\) повернуть на \(90^\circ\), получим направление \(m\). Значит, чтобы перейти от направления \(l\) к направлению \(m\), нужен поворот на \(90^\circ\), поэтому угол между \(l\) и \(m\) равен \(90^\circ\), то есть \(l \perp m\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!