
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 509 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
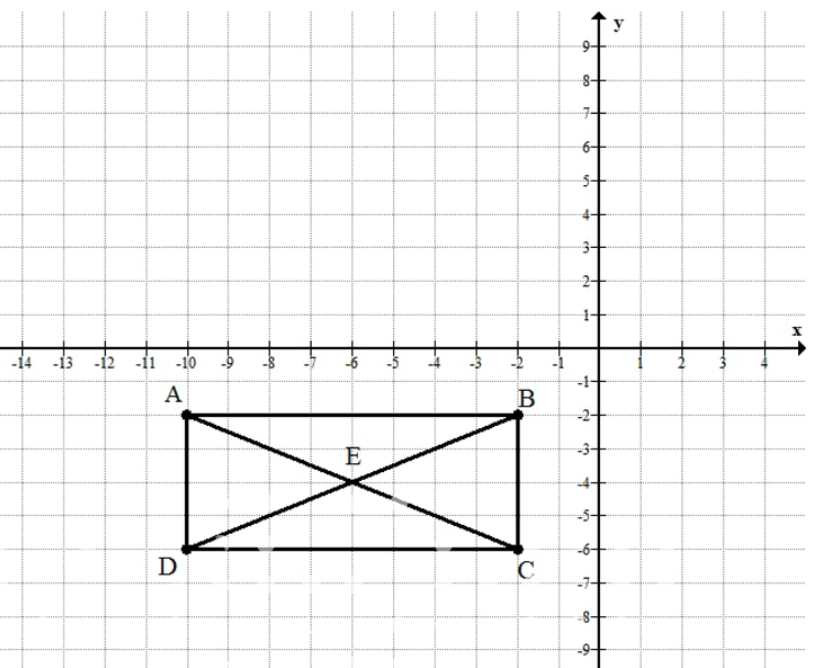
Постройте на координатной плоскости четырёхугольник \(ABCD\), если \(A(-10;-2)\), \(B(-2;-2)\), \(C(-2;-6)\), \(D(-10;-6)\). Является ли он прямоугольником? квадратом? Найдите периметр и площадь этого четырёхугольника, если единичный отрезок равен 1 см. Проведите отрезки \(AC\) и \(BD\) и найдите координаты точки пересечения \(E\) этих отрезков.
Длины сторон: \(AB=|-2-(-10)|=8\), \(BC=|-6-(-2)|=4\); значит \(ABCD\) — прямоугольник.
1) Периметр \(ABCD\): \(P=2(AB+BC)=2(8+4)=24\) (см).
2) Площадь \(ABCD\): \(S=AB\cdot BC=8\cdot 4=32\) (см\(^2\)).
3) Точка пересечения диагоналей: \(E\left(\frac{-10+(-2)}{2};\frac{-2+(-6)}{2}\right)=(-6;-4)\).
1) Периметр \(ABCD\) равен:
Сначала находим длины сторон по координатам, потому что стороны прямоугольника на рисунке параллельны осям: \(A(-10;-2)\), \(B(-2;-2)\) имеют одинаковую \(y\), значит \(AB\) — горизонтальный отрезок. Его длина равна разности абсцисс: \(AB=|-2-(-10)|=8\).
Аналогично \(B(-2;-2)\) и \(C(-2;-6)\) имеют одинаковую \(x\), значит \(BC\) — вертикальный отрезок. Его длина равна разности ординат: \(BC=|-6-(-2)|=4\). Тогда периметр прямоугольника \(P=2(AB+BC)=2(8+4)=24\) (см).
2) Площадь \(ABCD\) равна:
Так как \(ABCD\) — прямоугольник, его площадь равна произведению двух соседних сторон. Мы уже нашли их длины по координатам: \(AB=8\) и \(BC=4\). Это именно ширина и высота прямоугольника, потому что одна сторона горизонтальная, другая вертикальная.
Следовательно, \(S=AB\cdot BC=8\cdot 4=32\) (см\(^2\)). Это совпадает с тем, что площадь прямоугольника равна количеству единичных квадратов, укладывающихся в фигуру при сторонах \(8\) и \(4\).
3) Точка пересечения диагоналей \(E(-6;-4)\).
В прямоугольнике диагонали пересекаются и делятся пополам, поэтому точка пересечения диагоналей — это середина как диагонали \(AC\), так и диагонали \(BD\). Удобно взять диагональ \(AC\) с концами \(A(-10;-2)\) и \(C(-2;-6)\) и найти координаты середины.
Координаты середины отрезка находятся как средние арифметические координат концов: \(x_E=\frac{-10+(-2)}{2}=\frac{-12}{2}=-6\), \(y_E=\frac{-2+(-6)}{2}=\frac{-8}{2}=-4\). Значит, \(E(-6;-4)\), что совпадает с точкой на чертеже.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!