ГДЗ по Математике 6 Класс Часть 2 Номер 508 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

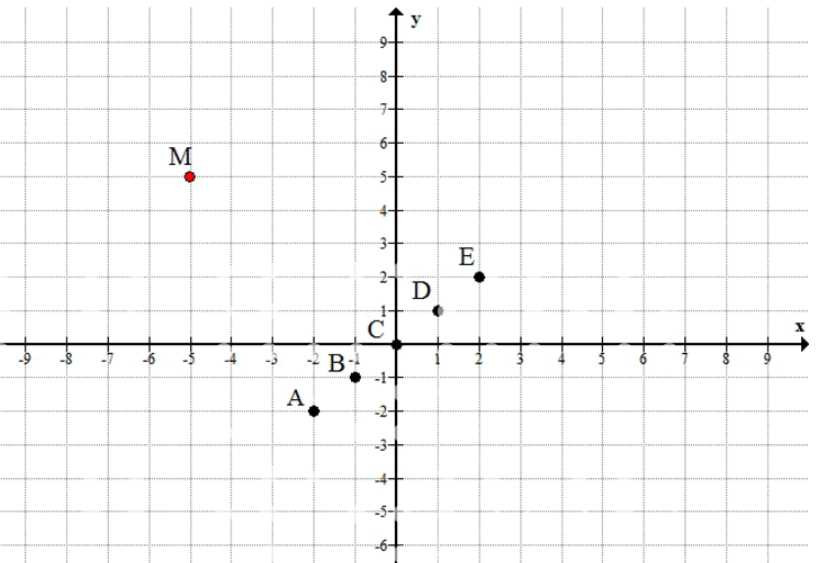
Изобразите на координатной плоскости точки \(A(-2;-2)\), \(B(-1;-1)\), \(C(0;0)\), \(D(1;1)\), \(E(2;2)\). Проверьте с помощью линейки, лежат ли эти точки на одной прямой и лежит ли на этой прямой точка \(M(-5;5)\).

Точки \(A(-2;-2)\), \(B(-1;-1)\), \(C(0;0)\), \(D(1;1)\), \(E(2;2)\) удовлетворяют условию \(y=x\), значит они лежат на прямой \(y=x\).

Для \(M(-5;5)\) должно быть \(y=x\), но \(5\ne -5\), поэтому точка \(M\) не лежит на этой прямой.

а) Чтобы проверить, лежат ли точки \(A(-2;-2)\), \(B(-1;-1)\), \(C(0;0)\), \(D(1;1)\), \(E(2;2)\) на одной прямой, удобно заметить общий признак: для каждой из этих точек значения координат равны, то есть везде \(y=x\). Это означает, что все эти точки удовлетворяют уравнению одной и той же прямой \(y=x\), следовательно, они лежат на одной прямой.

Можно дополнительно убедиться через угловой коэффициент (наклон): если точки лежат на одной прямой, то наклон между любыми двумя из них одинаков. Например, между \(A(-2;-2)\) и \(B(-1;-1)\) наклон равен \(\frac{-1-(-2)}{-1-(-2)}=\frac{1}{1}=1\), а между \(B(-1;-1)\) и \(C(0;0)\) наклон \(\frac{0-(-1)}{0-(-1)}=\frac{1}{1}=1\). Поскольку наклон совпадает, точки действительно располагаются на одной прямой, и эта прямая имеет вид \(y=x\).

б) Для точки \(M(-5;5)\) проверяем то же самое условие принадлежности прямой \(y=x\): на этой прямой обязательно должно выполняться равенство координат \(y=x\). Подставляем координаты точки \(M\): получаем \(y=5\) и \(x=-5\), то есть требуется, чтобы было \(5=-5\).

Равенство \(5=-5\) неверно, значит условие \(y=x\) для точки \(M\) не выполняется, и поэтому \(M\) не лежит на прямой, на которой лежат точки \(A\), \(B\), \(C\), \(D\), \(E\). Это совпадает с рисунком: \(A\), \(B\), \(C\), \(D\), \(E\) идут по диагонали \(y=x\), а \(M\) находится в другой части координатной плоскости и не попадает на эту диагональ.