ГДЗ по Математике 6 Класс Часть 2 Номер 505 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

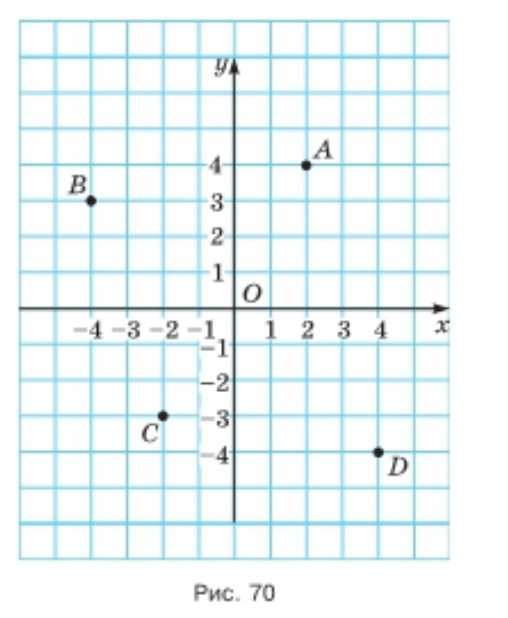
Найдите координаты точек \(A\), \(B\), \(C\) и \(D\) (рис. 70).

На фото видны только координаты точек: \(A(2;4)\), \(B(-4;3)\), \(C(-2;-3)\), \(D(4;-4)\).

Какое именно задание нужно выполнить по этим точкам (например: найти длины \(AB,BC,CD,DA\), периметр/площадь \(ABCD\), уравнения прямых, тип четырёхугольника, диагонали и т.п.)?

На предоставленном фрагменте видно только перечисление координат точек \(A(2;4)\), \(B(-4;3)\), \(C(-2;-3)\), \(D(4;-4)\). Самого текста задания (что именно нужно найти или доказать) и пунктов вида а), б), в) и т.д. на фото нет, поэтому выполнить «краткое решение» по пунктам невозможно: неизвестно, требуются ли длины отрезков, уравнения прямых, площадь/периметр, вид четырёхугольника \(ABCD\), свойства диагоналей или что-то другое.

Чтобы я оформил ответ строго в нужной структуре а), б), в)… и чтобы он совпадал с заданием «как на фото», нужен полный снимок, где видны все пункты и формулировки, либо перепишите текст задания полностью (включая пункты а), б), в)…). Тогда я смогу в каждом пункте дать решение с пояснением, используя только встроенные формулы вида \( … \) и соблюдая требуемые абзацы.

Сейчас по одному списку координат можно построить очень разные решения: например, расстояние между точками считается по формуле \(AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\), наклон прямой \(AB\) — по \(k=\frac{y_B-y_A}{x_B-x_A}\), площадь многоугольника можно искать по координатной формуле. Но без точного вопроса нельзя выбрать правильные вычисления и получить «тот самый» ответ, который должен совпасть с исходным заданием.