ГДЗ по Математике 6 Класс Часть 2 Номер 504 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

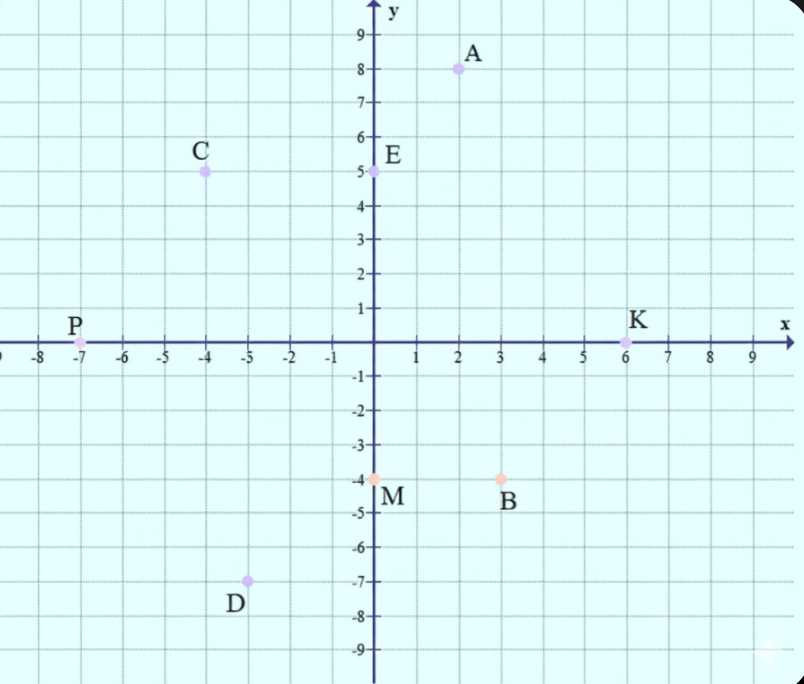
Постройте координатные прямые \(x\) и \(y\) и отметьте точки \(A(2;8)\), \(B(3;-4)\), \(C(-4;5)\), \(D(-3;-7)\), \(E(0;5)\), \(M(0;-4)\), \(K(6;0)\), \(P(-7;0)\).

Проведите оси координат \(x\) (горизонтальная) и \(y\) (вертикальная), отметьте начало координат \(O(0;0)\) и единичные отрезки.

Точки с \(x>0\) ставятся справа от оси \(y\), с \(x<0\) — слева; точки с \(y>0\) — выше оси \(x\), с \(y<0\) — ниже.

\(A(2;8)\) — в I четверти: от \(O\) 2 вправо и 8 вверх.
\(B(3;-4)\) — в IV четверти: от \(O\) 3 вправо и 4 вниз.
\(C(-4;5)\) — во II четверти: от \(O\) 4 влево и 5 вверх.
\(D(-3;-7)\) — в III четверти: от \(O\) 3 влево и 7 вниз.

\(E(0;5)\) лежит на оси \(y\) (так как \(x=0\)): на 5 вверх от \(O\).
\(M(0;-4)\) лежит на оси \(y\): на 4 вниз от \(O\).
\(K(6;0)\) лежит на оси \(x\) (так как \(y=0\)): на 6 вправо от \(O\).
\(P(-7;0)\) лежит на оси \(x\): на 7 влево от \(O\).

а) Постройте ось \(x\) как горизонтальную прямую со стрелкой вправо и ось \(y\) как вертикальную прямую со стрелкой вверх. Точка пересечения осей — начало координат \(O(0;0)\); это опорная точка, от которой откладываются все перемещения по координатам.

Выберите единичный отрезок (например, 1 клетка тетради) и одинаково отложите его на обеих осях, чтобы разметка была согласованной. Далее правило такое: сначала смотрим на \(x\) (движение вправо при \(x>0\) и влево при \(x<0\)), затем на \(y\) (движение вверх при \(y>0\) и вниз при \(y<0\)); если \(x=0\), точка лежит на оси \(y\), если \(y=0\), точка лежит на оси \(x\).

б) Для точки \(A(2;8)\) координата \(x=2\) означает, что от начала \(O(0;0)\) нужно пройти 2 единицы вправо вдоль оси \(x\) (положительное направление), а координата \(y=8\) означает затем подняться на 8 единиц вверх (положительное направление оси \(y\)).

Так как одновременно выполняется \(x>0\) и \(y>0\), точка \(A(2;8)\) находится в I четверти. На рисунке удобно сначала отметить на оси \(x\) отметку \(2\), из нее провести мысленную вертикаль, а на оси \(y\) отметить \(8\) и провести мысленную горизонталь; их пересечение и есть \(A\).

в) Для точки \(B(3;-4)\) сначала откладываем \(x=3\): от \(O(0;0)\) 3 единицы вправо. После этого учитываем \(y=-4\): отрицательное значение означает движение вниз, поэтому от полученного положения опускаемся на 4 единицы.

Здесь \(x>0\), но \(y<0\), значит точка лежит в IV четверти. Чтобы не перепутать знак, полезно помнить: минус у \(y\) всегда уводит ниже оси \(x\), поэтому \(B(3;-4)\) окажется ниже горизонтальной оси и правее вертикальной.

г) Для точки \(C(-4;5)\) координата \(x=-4\) задает движение влево от начала координат на 4 единицы (отрицательное направление оси \(x\)). Затем координата \(y=5\) задает движение вверх на 5 единиц (положительное направление оси \(y\)).

Так как \(x<0\) и \(y>0\), точка \(C(-4;5)\) находится во II четверти. При построении удобно сначала найти на оси \(x\) отметку \(-4\), а затем от нее подняться вверх до уровня \(y=5\), сохраняя строго вертикальное направление, чтобы координата \(x\) не изменилась.

д) Для точки \(D(-3;-7)\) выполняем два шага: \(x=-3\) — это 3 единицы влево от \(O(0;0)\), а \(y=-7\) — это 7 единиц вниз. Оба значения отрицательные, поэтому оба перемещения идут в отрицательных направлениях соответствующих осей.

Так как \(x<0\) и \(y<0\), точка \(D(-3;-7)\) лежит в III четверти. Проверка на рисунке простая: точка должна оказаться и левее оси \(y\), и ниже оси \(x\); если хотя бы одно из этих условий не выполнено, значит знак одной из координат учтен неверно.

е) Для точки \(E(0;5)\) первая координата равна нулю: \(x=0\). Это означает, что точка не смещается ни вправо, ни влево от оси \(y\), то есть она лежит прямо на оси \(y\).

Далее учитываем \(y=5\): от начала координат поднимаемся на 5 единиц вверх и ставим точку на самой оси \(y\). Важно не относить \(E(0;5)\) ни к одной из четвертей: точки на осях (кроме начала координат) не принадлежат четвертям, потому что для четверти нужно, чтобы \(x\neq 0\) и \(y\neq 0\).

ж) Для точки \(M(0;-4)\) снова \(x=0\), значит точка лежит на оси \(y\). Поэтому вся работа сводится к тому, чтобы правильно учесть знак второй координаты.

Так как \(y=-4\), от \(O(0;0)\) нужно опуститься на 4 единицы вниз по оси \(y\) и поставить точку \(M(0;-4)\). Полезная самопроверка: точка должна находиться на вертикальной оси и ниже оси \(x\), потому что отрицательный \(y\) всегда ниже.

з) Для точки \(K(6;0)\) вторая координата равна нулю: \(y=0\). Это означает, что точка лежит на оси \(x\), так как нет смещения вверх или вниз от горизонтальной оси.

Координата \(x=6\) положительная, поэтому от \(O(0;0)\) откладываем 6 единиц вправо по оси \(x\) и отмечаем \(K(6;0)\) на самой оси. Аналогично предыдущим случаям, \(K(6;0)\) не принадлежит четвертям, так как \(y=0\).

и) Для точки \(P(-7;0)\) также имеем \(y=0\), значит точка лежит на оси \(x\). Остается правильно отложить значение \(x\) с учетом знака.

Так как \(x=-7\), от начала координат идем на 7 единиц влево по оси \(x\) и ставим \(P(-7;0)\). Самопроверка: точка должна оказаться на горизонтальной оси и левее оси \(y\), потому что отрицательный \(x\) всегда слева.