ГДЗ по Математике 6 Класс Часть 2 Номер 495 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

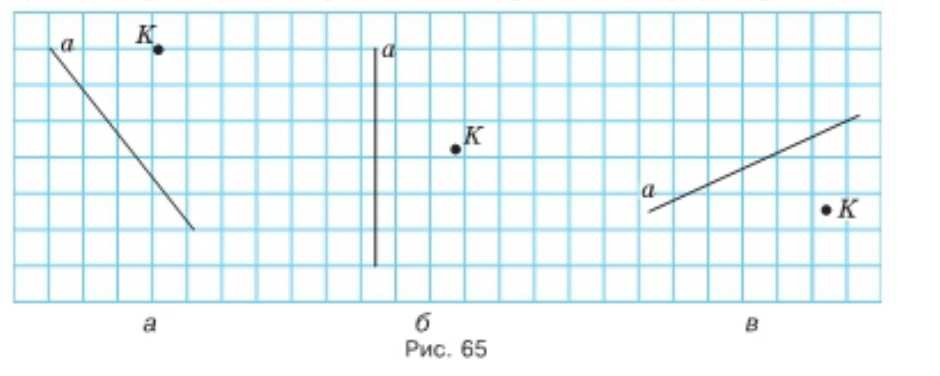
Перечертите рисунок 65 в тетрадь. Проведите через точку \(K\) прямую: а) параллельную прямой \(a\); б) перпендикулярную прямой \(a\).

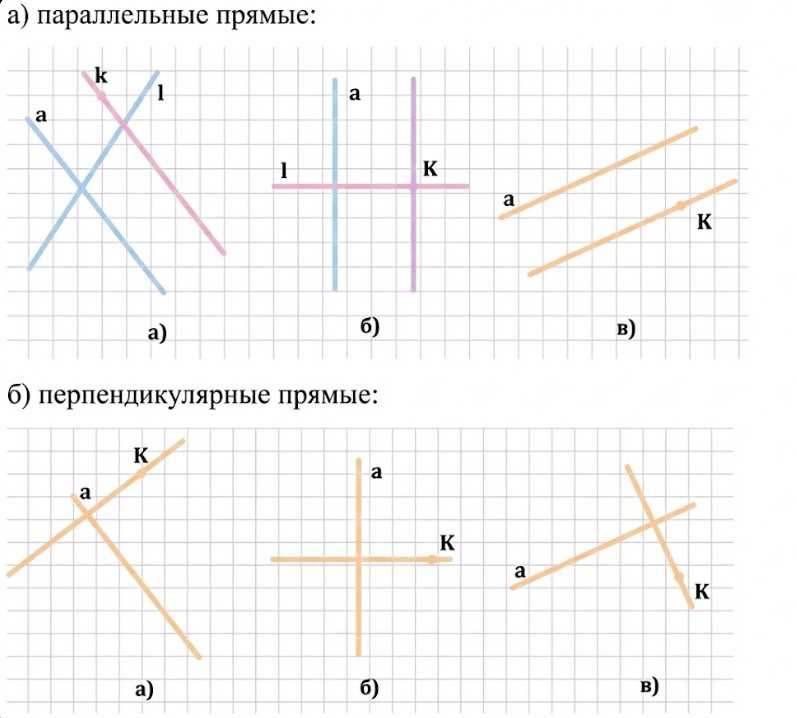
а) а) Прямые \(a\) и \(k\) параллельны, так как имеют одинаковое направление и не пересекаются.

б) Прямые \(a\) и \(k\) параллельны, так как обе вертикальные и не пересекаются.

в) Прямые \(a\) и \(k\) параллельны, так как имеют одинаковый наклон (угол наклона одинаков) и не пересекаются.

б) а) Прямые \(a\) и \(k\) перпендикулярны, так как пересекаются под углом \(90^\circ\).

б) Прямые \(a\) и \(k\) перпендикулярны, так как одна вертикальная, другая горизонтальная, значит угол между ними \(90^\circ\).

в) Прямые \(a\) и \(k\) перпендикулярны, так как пересекаются под углом \(90^\circ\).

а) На рисунке видно, что обе прямые \(a\) и \(k\) идут «в одном и том же направлении»: при движении вдоль одной из них влево-вправо вторая линия наклонена так же, без изменения угла наклона. Это означает, что углы наклона относительно горизонтали равны, а значит прямые имеют одинаковое направление.

Так как направления одинаковые, прямые при продолжении не пересекутся. Если бы они не были параллельны, то обязательно встретились бы в некоторой точке (пересеклись), но на чертеже они всюду сохраняют одинаковое расстояние друг от друга, следовательно \(a \parallel k\).

б) Здесь прямая \(a\) изображена вертикально, и прямая \(k\) тоже вертикальная. Вертикальные прямые имеют одно и то же направление: они параллельны оси \(Oy\) (то есть направлены «вверх-вниз»), поэтому их наклон одинаков.

Так как обе прямые вертикальные и расположены на некотором расстоянии друг от друга, они не пересекаются ни в одной точке. У вертикальных прямых нет «схождения» при продолжении, поэтому получаем \(a \parallel k\).

в) На рисунке обе прямые наклонены вверх вправо под одинаковым углом: это видно по тому, что они «повторяют» друг друга, как две рельсы, и расстояние между ними сохраняется по всей длине. Одинаковый наклон означает одинаковое направление.

Если продлить эти прямые, они не пересекутся, потому что при одинаковом направлении одна не «поворачивает» к другой. Следовательно, \(a \parallel k\).

а) В этом случае прямые \(a\) и \(k\) пересекаются, и место пересечения образует «крест» с прямым углом. Признак перпендикулярности: если угол между прямыми равен \(90^\circ\), то прямые перпендикулярны.

По рисунку видно, что одна прямая идет так, что образует с другой именно прямой угол (не острый и не тупой), то есть угол в точке пересечения равен \(90^\circ\). Значит, \(a \perp k\).

б) Здесь одна прямая вертикальная, а другая горизонтальная. Вертикальная прямая образует с горизонтальной прямой прямой угол, потому что они направлены взаимно перпендикулярно: одна «вверх-вниз», другая «влево-вправо».

В точке пересечения таких прямых получается угол \(90^\circ\). Поэтому по определению перпендикулярности имеем \(a \perp k\).

в) На рисунке прямые \(a\) и \(k\) пересекаются под углом, который выглядит как прямой: одна линия наклонена вверх вправо, а другая наклонена так, что «перекрывает» ее под прямым углом. Это соответствует ситуации, когда при повороте направления одной прямой на \(90^\circ\) получается направление другой.

Так как в точке пересечения образуется угол \(90^\circ\), прямые являются перпендикулярными. Следовательно, \(a \perp k\).