
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 494 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
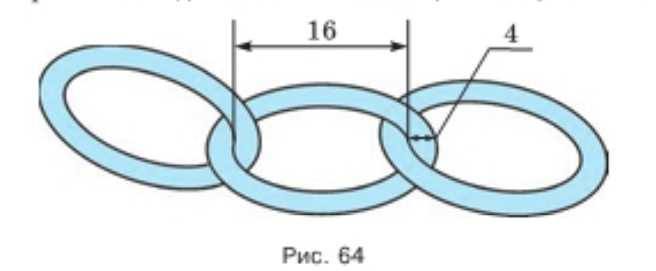
Из пятидесяти звеньев составлена цепь. Найдите длину этой цепи, если просвет каждого звена — 16 мм, а толщина — 4 мм (рис. 64).
Берём толщину начала цепи \(4\) мм, прибавляем \(50\) раз по \(16\) мм (просвет каждого звена) и прибавляем толщину конца цепи \(4\) мм.
Длина цепи: \(4+50\cdot 16+4=4+800+4=808\) мм \(=80\) см \(8\) мм.
Ответ: \(80\) см \(8\) мм.
В этой задаче длина цепи складывается из трёх частей: толщины первого края, суммарных «просветов» звеньев и толщины последнего края. По условию толщина начала цепи равна \(4\) мм, и такую же толщину \(4\) мм даёт конец цепи, потому что цепь имеет два края, которые добавляют длину.
Далее учитываем вклад звеньев по их просветам: сказано, что таких одинаковых участков \(50\), и каждый даёт по \(16\) мм длины. Поэтому общая длина от этих участков равна \(50\cdot 16\) мм. Толщину колец дополнительно не прибавляем, так как звенья переплетены между собой, и в длину цепи по прямой в расчёте уже заложены именно просветы звеньев, а не отдельные толщины каждого кольца.
Собираем всё вместе: \(4+50\cdot 16+4\). Сначала находим произведение \(50\cdot 16=800\), затем прибавляем толщины краёв: \(4+800+4=808\) мм. Переводим миллиметры в сантиметры: \(808\) мм \(=80\) см \(8\) мм, так как \(80\) см \(=800\) мм и остаётся \(8\) мм.
Ответ: \(80\) см \(8\) мм.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!