ГДЗ по Математике 6 Класс Часть 2 Номер 486 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

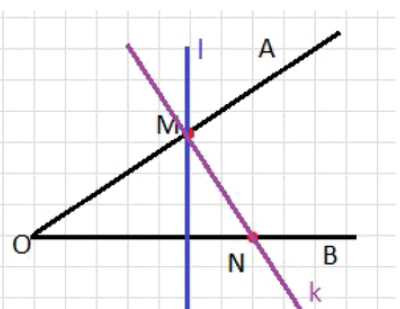
Постройте угол \(AOB\), равный \(35^\circ\). Отметьте точку \(M\) на стороне \(OA\) и точку \(N\) на стороне \(OB\). Проведите через точку \(M\) прямую, перпендикулярную стороне \(OB\), а через точку \(N\) прямую, перпендикулярную стороне \(OA\).

Так как \(l\perp OB\) и \(k\perp OA\), то угол между прямыми \(l\) и \(k\) равен углу между прямыми \(OB\) и \(OA\) (поворот обеих сторон на \(90^\circ\) не меняет величину угла).

Следовательно, \(\angle(l,k)=\angle AOB\).

а) По рисунку дано, что прямая \(l\) перпендикулярна \(OB\), то есть угол между \(l\) и \(OB\) равен \(90^\circ\): \(l\perp OB\). Также дано, что прямая \(k\) перпендикулярна \(OA\), то есть угол между \(k\) и \(OA\) тоже равен \(90^\circ\): \(k\perp OA\). Эти условия означают, что \(l\) получена из \(OB\) поворотом на \(90^\circ\) (в одну из сторон), и \(k\) получена из \(OA\) поворотом на \(90^\circ\) (тоже в одну из сторон).

Если обе стороны угла повернуть на один и тот же угол, величина угла между ними не изменится. Здесь луч \(OB\) заменяется на перпендикуляр \(l\), а луч \(OA\) заменяется на перпендикуляр \(k\); то есть оба направления «сдвинуты» на \(90^\circ\), поэтому относительное положение прямых сохраняет ту же величину угла.

Значит, угол между прямыми \(l\) и \(k\) равен углу между прямыми \(OB\) и \(OA\), то есть \(\angle(l,k)=\angle AOB\).