
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 485 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
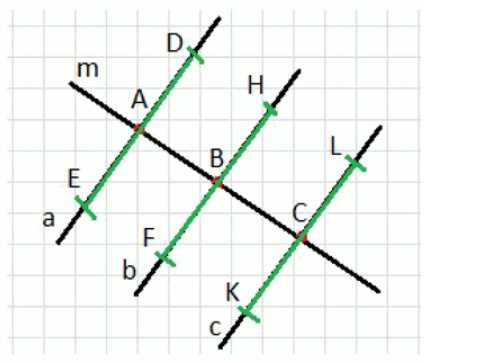
Начертите прямую \(m\) и отметьте на ней три точки — \(A\), \(B\) и \(C\). Через эти точки проведите прямые, перпендикулярные прямой \(m\). Отметьте на этих прямых параллельные отрезки.
Так как \(a \perp m\), \(b \perp m\), \(c \perp m\), то прямые \(a\), \(b\), \(c\) параллельны (две прямые, перпендикулярные одной и той же прямой, параллельны), значит \(a \parallel b \parallel c\).
Отрезки \(ED\), \(FH\), \(KL\) лежат соответственно на прямых \(a\), \(b\), \(c\), поэтому \(ED \parallel FH \parallel KL\).
Из условия \(a \perp m\), \(b \perp m\), \(c \perp m\) видно, что каждая из прямых \(a\), \(b\), \(c\) образует с прямой \(m\) прямой угол \(90^\circ\). То есть направление каждой из этих прямых «фиксировано» относительно \(m\): все они перпендикулярны одной и той же прямой \(m\).
Если две прямые на плоскости перпендикулярны одной и той же прямой, то они параллельны друг другу, потому что каждая из них образует с этой прямой одинаковый угол \(90^\circ\). Поэтому из \(a \perp m\) и \(b \perp m\) получаем \(a \parallel b\); аналогично из \(b \perp m\) и \(c \perp m\) получаем \(b \parallel c\), а значит \(a \parallel b \parallel c\).
На рисунке отрезок \(ED\) лежит на прямой \(a\), то есть прямая, содержащая \(ED\), совпадает по направлению с \(a\). Аналогично, отрезок \(FH\) лежит на прямой \(b\), а отрезок \(KL\) лежит на прямой \(c\), значит направления \(ED\), \(FH\), \(KL\) совпадают соответственно с направлениями \(a\), \(b\), \(c\).
Так как уже установлено \(a \parallel b \parallel c\), то все отрезки, лежащие на этих прямых, также параллельны друг другу (параллельность отрезков понимается как параллельность прямых, на которых они расположены). Следовательно, \(ED \parallel FH \parallel KL\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!