
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 483 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
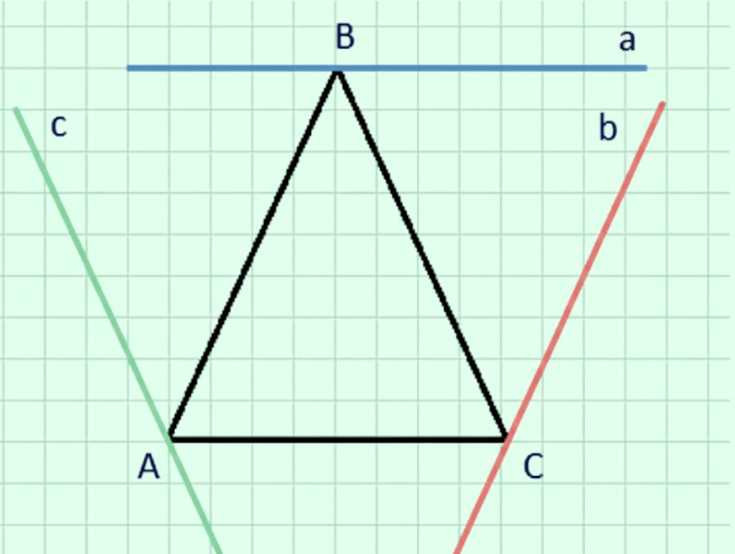
Начертите треугольник и проведите через каждую вершину прямую, параллельную противоположной стороне.
По рисунку прямая \(a\) проведена через точку \(B\) горизонтально так же, как основание \(AC\), поэтому \(a \parallel AC\).
Прямая \(b\) имеет то же направление (наклон), что и сторона \(AB\), следовательно \(b \parallel AB\).
Прямая \(c\) проведена с тем же наклоном, что и сторона \(BC\), поэтому \(c \parallel BC\).
По рисунку нужно установить параллельность прямых \(a\), \(b\), \(c\) сторонам треугольника \(ABC\). Для этого достаточно сравнить направления: параллельные прямые на клетчатой сетке имеют одинаковый наклон (идут «одинаково» относительно горизонтали и вертикали) и при продолжении не пересекаются.
Прямая \(a\) проходит через точку \(B\) и нарисована горизонтально. Основание треугольника \(AC\) тоже горизонтальное (точки \(A\) и \(C\) лежат на одной горизонтальной линии сетки), значит обе прямые имеют нулевой наклон и одинаковое направление, поэтому \(a \parallel AC\).
Прямая \(b\) (красная) проведена рядом со стороной \(AB\) так, что наклон у неё совпадает с наклоном \(AB\): при движении вверх по \(b\) мы смещаемся вправо на столько же «клеток», как и при движении вверх по \(AB\). Раз направление совпадает, эти прямые не могут пересечься и являются параллельными, значит \(b \parallel AB\).
Прямая \(c\) (зелёная) имеет тот же наклон, что и сторона \(BC\): при движении вверх по \(c\) происходит такое же смещение влево, как и при движении вверх по \(BC\). Одинаковый наклон означает одинаковое направление, следовательно прямые параллельны, то есть \(c \parallel BC\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!