
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 478 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
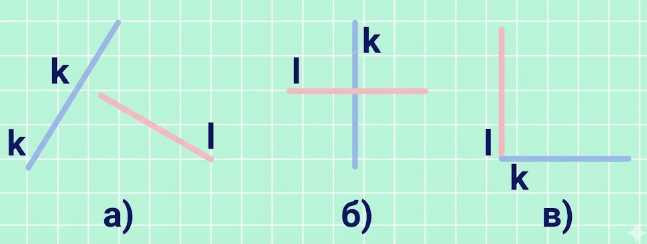
Начертите два перпендикулярных луча так, чтобы они:
а) не пересекались; б) пересекались; в) имели общее начало.
а) Не пересекались: на рисунке \(l\) и \(k\) расположены раздельно, общих точек нет.
б) Пересекались: \(l\) и \(k\) пересекаются в одной точке (крест).
в) Имели общее начало: \(l\) и \(k\) выходят из одной точки (общая начальная точка).
а) Чтобы проверить, пересекаются ли два луча \(l\) и \(k\), смотрим, есть ли у них хотя бы одна общая точка. Пересечение означает, что существует точка \(P\), которая лежит одновременно на обоих лучах, то есть \(P \in l\) и \(P \in k\).
На рисунке в пункте а) лучи направлены в разные стороны и расположены так, что ни одна их часть не проходит через одну и ту же точку. Поэтому общих точек нет, то есть \(l \cap k = \emptyset\), следовательно, лучи не пересекаются.
б) Пересечение лучей означает наличие общей точки, в которой они «встречаются». Достаточно одной общей точки \(P\), чтобы сказать, что лучи пересекаются: \(P \in l\) и \(P \in k\).
На рисунке в пункте б) видно, что лучи образуют крест: вертикальный и горизонтальный лучи проходят через одну и ту же центральную точку. Значит, существует общая точка пересечения \(P\), поэтому \(l \cap k \neq \emptyset\), и лучи пересекаются.
в) «Иметь общее начало» означает, что начальные точки лучей совпадают. Если начало луча \(l\) — точка \(O\), и начало луча \(k\) — тоже точка \(O\), то говорят, что у лучей общее начало; при этом направления лучей могут быть разными.
На рисунке в пункте в) оба луча выходят из одной точки (виден общий «угол»): один луч идёт вертикально, другой горизонтально, но стартуют они из одной и той же точки \(O\). Поэтому начала совпадают: начало \(l\) равно началу \(k\), то есть у них общее начало.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!