
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 476 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
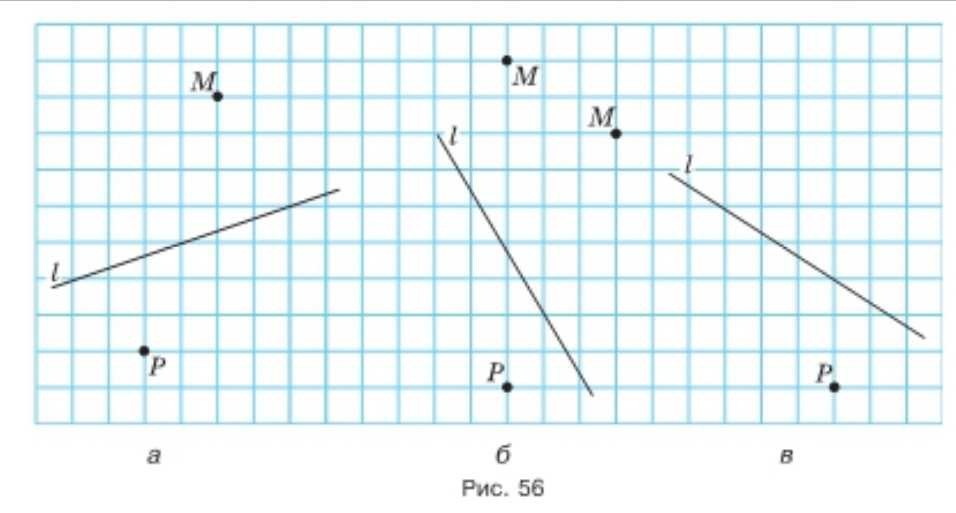
Перечертите рисунок 56 в тетрадь. Проведите через точки \(M\) и \(P\) прямые, перпендикулярные прямой \(l\).
а) Через точку \(M\) проведите прямую \(m\), перпендикулярную прямой \(l\): \(m \perp l\). Через точку \(P\) проведите прямую \(p\), перпендикулярную прямой \(l\): \(p \perp l\).
б) Через точку \(M\) проведите прямую \(m\), перпендикулярную прямой \(l\): \(m \perp l\). Через точку \(P\) проведите прямую \(p\), перпендикулярную прямой \(l\): \(p \perp l\).
в) Через точку \(M\) проведите прямую \(m\), перпендикулярную прямой \(l\): \(m \perp l\). Через точку \(P\) проведите прямую \(p\), перпендикулярную прямой \(l\): \(p \perp l\).
а) Сначала на рисунке найдите прямую \(l\) и точки \(M\) и \(P\). Задача просит через каждую из этих точек провести прямую, которая образует с \(l\) прямой угол, то есть требуется построить перпендикуляры к \(l\). Поэтому в этом пункте нужно выполнить два одинаковых по смыслу построения: одно через \(M\), другое через \(P\).
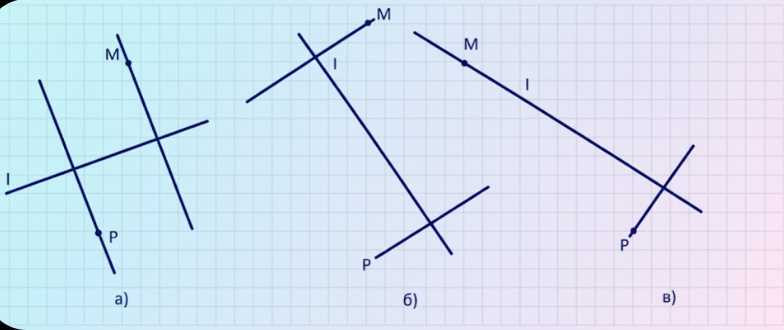
Через точку \(M\) проводим прямую так, чтобы угол между ней и \(l\) был \(90^\circ\); это и означает условие перпендикулярности \(m \perp l\). Аналогично через точку \(P\) проводим прямую, которая тоже образует с \(l\) угол \(90^\circ\), получаем \(p \perp l\). В результате на чертеже появятся две прямые \(m\) и \(p\), каждая из которых пересекает \(l\) под прямым углом и проходит соответственно через заданные точки.
б) В этом рисунке прямая \(l\) имеет другое положение, но требование не меняется: нужно через данные точки \(M\) и \(P\) провести перпендикуляры к \(l\). Сначала отмечаем, что перпендикуляр к \(l\) — это любая прямая, пересекающая \(l\) под углом \(90^\circ\), и при этом проходящая через указанную точку. Поэтому снова строим две прямые: одну через \(M\), другую через \(P\).
Через \(M\) проводим прямую \(m\) так, чтобы \(m \perp l\); на клетчатой сетке удобно контролировать прямой угол по направлению \(l\): новая прямая должна быть к ней «поперечной» под \(90^\circ\). Затем через \(P\) проводим прямую \(p\) с тем же условием \(p \perp l\). После построения обязательно проверяем по рисунку: обе прямые пересекают \(l\) и образуют с ней прямой угол, а точки \(M\) и \(P\) лежат на своих прямых.
в) Здесь также дана прямая \(l\) и две точки \(M\) и \(P\), расположенные по-своему относительно \(l\). Требуется ровно то же действие: через каждую точку провести единственную прямую, перпендикулярную \(l\). Смысл построения в том, что через заданную точку можно провести ровно один перпендикуляр к данной прямой, поэтому результат однозначен.
Сначала через точку \(M\) проводим прямую \(m\), добиваясь условия \(m \perp l\), то есть угла \(90^\circ\) при пересечении с \(l\). Затем через точку \(P\) проводим прямую \(p\) так, чтобы \(p \perp l\). На готовом чертеже должно получиться: \(M \in m\), \(P \in p\), и каждая из прямых \(m\) и \(p\) пересекает \(l\) под прямым углом.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!