ГДЗ по Математике 6 Класс Часть 2 Номер 466 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

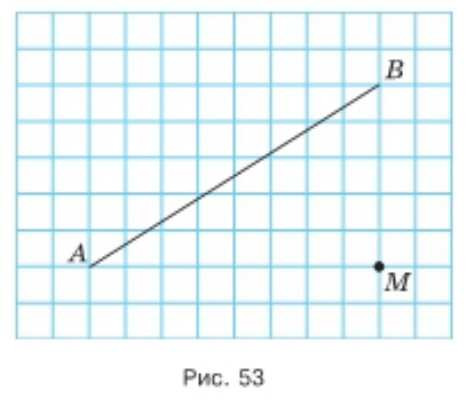
Начертите в тетради прямую \(AB\) и отметьте точку \(M\) так, как показано на рисунке 53. Проведите через точку \(M\) перпендикуляр к прямой \(AB\).

Приложите угольник одной стороной к прямой \(AB\).

Не отрывая угольник, сдвиньте его вдоль \(AB\) так, чтобы другая сторона угольника проходила через точку \(M\).

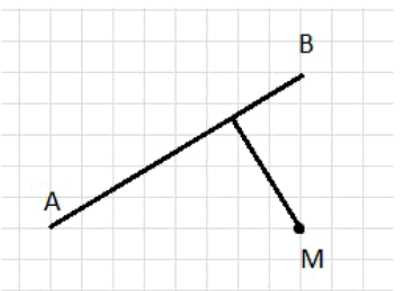
Проведите через \(M\) линию по этой стороне угольника; полученная прямая перпендикулярна \(AB\), то есть \(MN \perp AB\).

а) Начертите в тетради прямую \(AB\) и отметьте точку \(M\) так, как на рисунке: точка \(M\) должна находиться не на прямой \(AB\), а ниже неё (как показано), чтобы было видно, что перпендикуляр будет «падать» на прямую \(AB\). Чтобы прямая \(AB\) получилась похожей на рисунок, удобно провести её наклонно: отметьте две точки на листе и соедините их линейкой, затем подпишите левый конец как \(A\), правый как \(B\).

Далее отметьте точку \(M\) в стороне от прямой \(AB\) (по рисунку она расположена ближе к правой части, ниже прямой). Важно, чтобы \(M\) была отмечена точно и отчётливо, потому что через неё будет проходить строящаяся прямая. После этого можно лёгким штрихом прикинуть, в какую сторону от \(M\) будет идти перпендикуляр, чтобы он пересёк прямую \(AB\) примерно в той области, как на рисунке.

б) Чтобы провести через точку \(M\) перпендикуляр к прямой \(AB\), используйте угольник: приложите одну его сторону так, чтобы она точно совпала с направлением прямой \(AB\). Это означает, что ребро угольника должно «лежать» на прямой \(AB\) без перекоса: если есть линейка, можно сначала совместить линейку с \(AB\), а затем прижать угольник к линейке, чтобы сторона угольника не съехала с направления \(AB\).

Не меняя положения угольника относительно направления \(AB\), сдвиньте его вдоль прямой \(AB\) так, чтобы другая сторона угольника (та, что образует прямой угол с первой) прошла через точку \(M\). Сдвигать нужно аккуратно: угол угольника должен оставаться ориентированным так же, как и был, иначе перпендикулярность нарушится. Когда увидите, что перпендикулярная сторона угольника проходит точно через точку \(M\), остановитесь и удерживайте угольник.

в) Проведите линию через точку \(M\) вдоль той стороны угольника, которая перпендикулярна прямой \(AB\). Линию лучше проводить по линейному краю угольника ровно, без отрыва, чтобы прямая получилась чёткой. Эта прямая пересечёт \(AB\) в некоторой точке (её можно не подписывать, но при желании можно обозначить, например, \(N\)).

Почему эта прямая действительно перпендикулярна \(AB\): в угольнике стороны, образующие прямой угол, всегда взаимно перпендикулярны. Раз одна сторона угольника совмещена с прямой \(AB\), то другая сторона автоматически образует с \(AB\) угол \(90^\circ\). Значит, проведённая через \(M\) прямая является перпендикуляром к \(AB\), то есть \(MN \perp AB\) (если точку пересечения обозначили как \(N\)).

г) Для самопроверки после построения можно ещё раз приложить угольник: совместите одну его сторону с прямой \(AB\), а вершину прямого угла подведите к месту пересечения построенной линии с \(AB\). Вторая сторона угольника должна совпасть с проведённой через \(M\) прямой — тогда видно, что угол между ними прямой, то есть равен \(90^\circ\).

Если при проверке видно, что проведённая линия чуть «не попадает» в направление перпендикулярной стороны угольника, значит, в момент построения угольник сдвинулся или был наклонён. Тогда лучше аккуратно провести линию заново, ориентируясь по угольнику, потому что условие задачи — провести именно перпендикуляр через точку \(M\) к прямой \(AB\).