
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 465 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
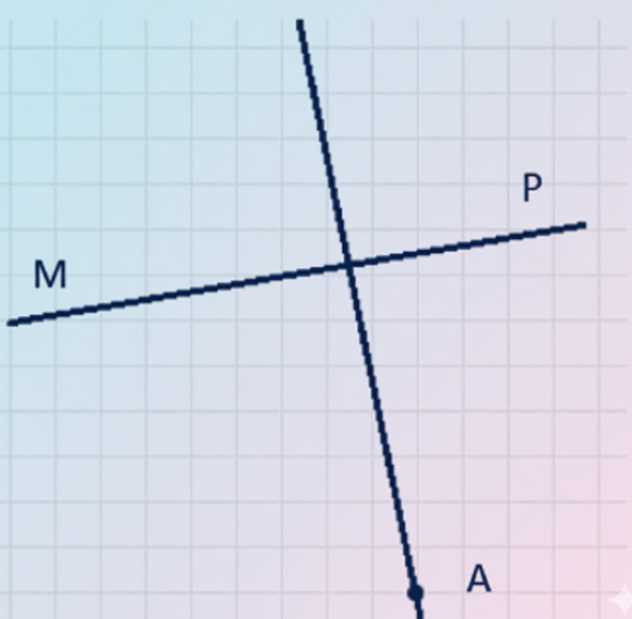
Начертите прямую \(MP\) и отметьте точку \(A\), не лежащую на этой прямой. Проведите с помощью чертёжного треугольника через точку \(A\) прямую, перпендикулярную прямой \(MP\). Сколько прямых, перпендикулярных \(MP\), можно провести через точку \(A\)?
Через точку \(A\), не лежащую на прямой \(MP\), по аксиоме перпендикуляра можно провести ровно одну прямую, перпендикулярную \(MP\).
Ответ: \(1\) прямая.
а) Точка \(A\) на рисунке не лежит на прямой \(MP\), то есть \(A \notin MP\). В евклидовой геометрии действует свойство: через точку, не лежащую на данной прямой, можно провести перпендикуляр к этой прямой.
Этот перпендикуляр существует и при этом единственный: если бы через \(A\) можно было провести две разные прямые, обе перпендикулярные \(MP\), то они обе образовывали бы с \(MP\) угол \(90^\circ\), а значит совпали бы, что противоречит тому, что они разные. Поэтому через точку \(A\) проводится ровно одна прямая, перпендикулярная прямой \(MP\), то есть ответ: \(1\) прямая.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!