ГДЗ по Математике 6 Класс Часть 2 Номер 463 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

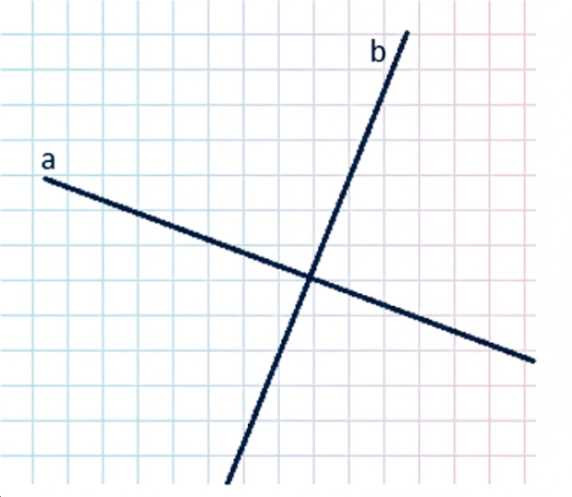
Постройте с помощью транспортира две перпендикулярные прямые.

Проведём прямую \(a\) на клетчатой бумаге, отметив две точки и соединив их линейкой.

Через точку пересечения построим прямую \(b\), перпендикулярную прямой \(a\): на сетке удобно выбрать направление так, чтобы при движении по \(a\) на несколько клеток вправо получалось движение на столько же клеток по \(b\) вверх (то есть направления взаимно перпендикулярны).

Получаем две пересекающиеся прямые \(a\) и \(b\) такие, что \(a \perp b\).

Построим первую прямую и обозначим её \(a\). На клетчатой бумаге для этого достаточно выбрать две точки на сетке и соединить их: через любые две разные точки проходит ровно одна прямая, поэтому линия получится однозначной и будет «продолжаться» в обе стороны.

Затем выберем на прямой \(a\) точку пересечения (удобно брать примерно середину рисунка, как на фото), через которую будет проходить вторая прямая. Требуется, чтобы вторая прямая \(b\) образовывала с \(a\) прямой угол, то есть выполнялось условие \(a \perp b\).

На клетчатой бумаге перпендикулярность удобно контролировать по «шагам» по клеткам. Если для направления прямой \(a\) от точки пересечения взять ход на \(p\) клеток вправо и на \(q\) клеток вниз (или вверх), то для перпендикулярного направления можно взять ход на \(q\) клеток вправо и на \(p\) клеток вверх (или вниз), то есть поменять местами числа шагов и изменить знак у одного из них; так получаются направления, образующие угол \(90^\circ\).

От точки пересечения откладываем выбранный «шаг» для прямой \(b\) в одну сторону, ставим точку, затем откладываем такой же шаг в противоположную сторону, ставим вторую точку. Соединяем эти две точки прямой линией — получается прямая \(b\), пересекающая \(a\) под прямым углом, как на рисунке.

Итог построения: получены две пересекающиеся прямые \(a\) и \(b\), причём \(a \perp b\).