ГДЗ по Математике 6 Класс Часть 2 Номер 4 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

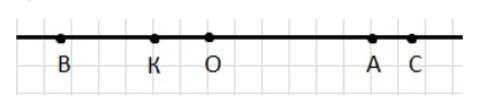
Проведите горизонтальную прямую и отметьте на ней точку O. Отметьте на этой прямой точки A, B, C и K, если известно, что:

а) A правее O на 6 клеток;

б) B левее O на 5,5 клетки;

в) C правее O на \(7\frac{1}{2}\) клетки;

г) K левее O на 2 клетки.

а) Точка \(A\) правее \(O\) на \(6\) клеток, значит от \(O\) отсчитываем \(6\) клеток вправо и ставим \(A\).

б) Точка \(B\) левее \(O\) на \(5{,}5\) клеток, значит от \(O\) отсчитываем \(5\) клеток и ещё \(0{,}5\) клетки влево и ставим \(B\).

в) Точка \(C\) правее \(O\) на \(7\frac{1}{2}\) клетки, то есть на \(7{,}5\) клеток, значит от \(O\) отсчитываем \(7\) клеток и ещё \(0{,}5\) клетки вправо и ставим \(C\).

г) Точка \(K\) левее \(O\) на \(2\) клетки, значит от \(O\) отсчитываем \(2\) клетки влево и ставим \(K\).

а) Сначала фиксируем точку \(O\) на данной прямой и считаем её «нулевой» точкой отсчёта: все перемещения вправо будем считать положительным направлением, а все перемещения влево — отрицательным. Условие «\(A\) правее \(O\) на 6 клеток» означает, что от отметки \(O\) нужно последовательно пройти 6 одинаковых промежутков сетки (6 клеток) вправо. Счёт ведём по вертикальным линиям сетки: переход от одной линии к соседней — это 1 клетка. После того как отсчитано ровно 6 клеток вправо от \(O\), в полученной точке ставим метку и подписываем её \(A\). В терминах расстояния это можно записать как \(OA=6\) (в клетках) и направление от \(O\) к \(A\) вправо.

б) Условие «\(B\) левее \(O\) на 5,5 клеток» означает перемещение от точки \(O\) влево на \(5{,}5\) клетки, то есть на \(5\) целых клеток и ещё на половину клетки. Практически это делается так: сначала от \(O\) отсчитываем 5 полных клеток влево (каждый раз переходя через одну вертикальную линию сетки), а затем от полученной точки смещаемся ещё на \(0{,}5\) клетки влево, то есть ровно до середины следующей клетки. Полученная позиция не попадает на целую вертикальную линию сетки, а находится посередине между двумя соседними линиями — это и соответствует половине клетки. В этой точке ставим метку и подписываем \(B\). Краткая запись условия расстояния: \(OB=5{,}5\) (в клетках) влево от \(O\).

в) Условие «\(C\) правее \(O\) на \(7\frac{1}{2}\) клетки» означает то же самое, что «на \(7{,}5\) клетки», так как \(7\frac{1}{2}=7+\frac{1}{2}=7{,}5\). Значит, от точки \(O\) сначала отсчитываем 7 полных клеток вправо, двигаясь по сетке так же, как в пункте а), а затем добавляем ещё половину клетки вправо, то есть смещаемся к середине следующего клеточного промежутка. Важно не перепутать: половина клетки — это середина между двумя соседними вертикальными линиями сетки, а не ещё одна полная клетка. В найденной точке ставим метку и подписываем \(C\). При проверке удобно помнить, что \(C\) должен оказаться правее \(A\), потому что \(7{,}5>6\).

г) Условие «\(K\) левее \(O\) на 2 клетки» выполняется самым прямым способом: от точки \(O\) отсчитываем 2 клетки влево, делая два равных шага по сетке (каждый шаг — 1 клетка). После двух шагов влево получаем точку, расположенную на вертикальной линии сетки (так как число клеток целое), и в этой точке ставим метку \(K\). Запись в терминах расстояния: \(OK=2\) (в клетках) влево от \(O\). Также видно, что \(K\) будет между \(O\) и \(B\), так как \(2<5{,}5\), то есть \(K\) ближе к \(O\), чем \(B\).