
ГДЗ к учебнику Виленкина для 6 класса, часть 2 (авторы: Жохов, Чесноков, Виленкин) — это системный помощник по темам второй половины курса, где расширяется и закрепляется база математических навыков: работа с десятичными дробями и процентами, действия с рациональными числами, пропорции и отношения, степенные выражения и делимость, задачи на скорость–время–расстояние, а также углубление в уравнения и текстовые задачи. Продуманный решебник следует логике учебника: показывает последовательность шагов, связывает каждое преобразование с теорией, тренирует аккуратность записи.
ГДЗ по Математике 6 Класс Часть 2 Номер 376 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы
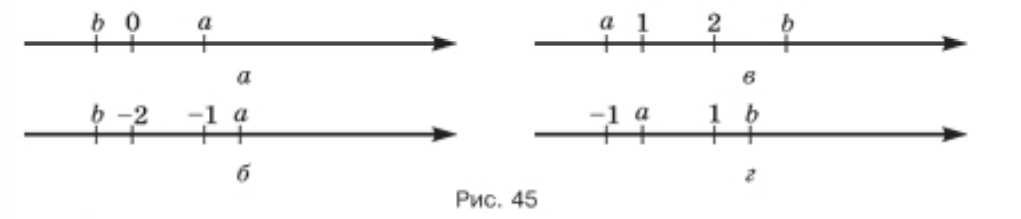
На координатной прямой (рис. 45) отмечены числа \(a\) и \(b\). Определите знак произведения \(ab\).
а) Так как \(a>0\) и \(b<0\), множители разных знаков. По правилу знаков произведение положительного и отрицательного — отрицательное, значит \(ab<0\).
б) Рассматриваем все варианты для \(a\) при условии \(b<0\). Если \(a<0\), то оба множителя отрицательные и \(ab>0\); если \(a=0\), то \(ab=0\); если \(a>0\), то знаки разные и \(ab<0\).
в) Рассматриваем все варианты для \(a\) при условии \(b>0\). Если \(a>0\), то оба множителя положительные и \(ab>0\); если \(a=0\), то \(ab=0\); если \(a<0\), то знаки разные и \(ab<0\).
г) При \(b=0\) произведение всегда равно нулю, потому что \(a\cdot 0=0\) при любом \(a\). Поэтому при \(a<0\), \(a=0\) и \(a>0\) во всех случаях \(ab=0\).
а) При умножении двух чисел знак произведения определяется так: если множители разных знаков, то произведение отрицательное. Здесь \(a>0\) — положительное число, а \(b<0\) — отрицательное, то есть знаки у множителей разные.
Поэтому произведение \(ab\) будет отрицательным: \(ab<0\). Это следует из общего правила: \(+\cdot — = -\), значит результат меньше нуля.
б) Здесь рассматривается случай \(b<0\) (второй множитель отрицателен), а знак \(a\) может быть разным. Удобно опираться на два правила: если множители одного знака, то произведение положительное, а если разных — отрицательное; отдельно помнить, что при наличии нуля произведение равно нулю.
Если \(a<0\) и \(b<0\), то оба множителя отрицательные, значит их произведение положительное: \(ab>0\). Если \(a=0\) и \(b<0\), то в произведении есть нулевой множитель, значит \(ab=0\) независимо от знака второго множителя. Если \(a>0\) и \(b<0\), множители разных знаков, поэтому \(ab<0\).
в) Здесь рассматривается случай \(b>0\) (второй множитель положителен), а \(a\) может быть положительным, нулём или отрицательным. Используем те же правила: одинаковые знаки дают положительное произведение, разные знаки — отрицательное, а наличие нуля даёт ноль.
Если \(a>0\) и \(b>0\), оба множителя положительные, значит \(ab>0\). Если \(a=0\) и \(b>0\), то \(ab=0\), потому что \(0\cdot b=0\). Если \(a<0\) и \(b>0\), множители разных знаков, поэтому произведение отрицательное: \(ab<0\).
г) Здесь рассматривается случай \(b=0\). Главное правило для этого пункта: если хотя бы один множитель равен нулю, то произведение равно нулю, потому что \(a\cdot 0=0\) при любом значении \(a\).
Поэтому при \(a<0\) и \(b=0\) получаем \(ab=0\). Аналогично, при \(a=0\) и \(b=0\) также \(ab=0\). И при \(a>0\) и \(b=0\) снова \(ab=0\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!