ГДЗ по Математике 6 Класс Часть 2 Номер 375 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

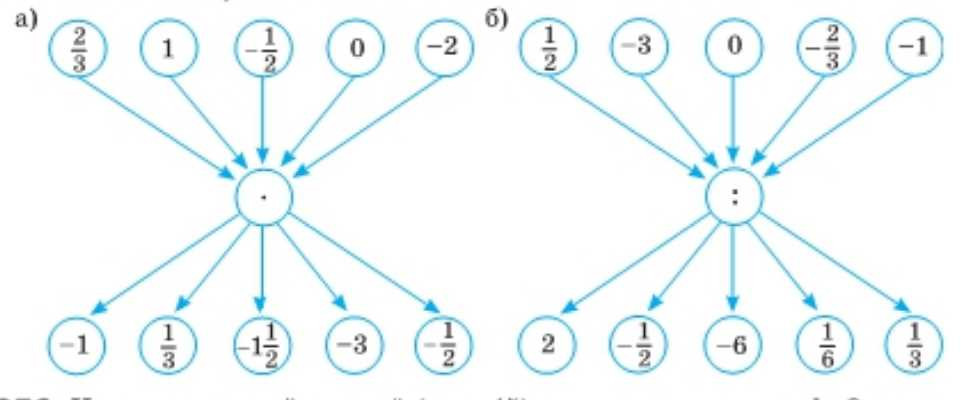
Вычислите устно:

а) Используем правила умножения: знак по правилу «одинаковые знаки — плюс, разные — минус», модули перемножаем; смешанное число переводим в неправильную дробь \( -1\frac{1}{2}=-\frac{3}{2} \). Тогда получаем: \(\frac{2}{3}\cdot(-1)=-\frac{2}{3}\), \(\frac{2}{3}\cdot\frac{1}{3}=\frac{2}{9}\), \(\frac{2}{3}\cdot\left(-1\frac{1}{2}\right)=\frac{2}{3}\cdot\left(-\frac{3}{2}\right)=-1\), \(\frac{2}{3}\cdot(-3)=-2\), \(\frac{2}{3}\cdot\left(-\frac{1}{2}\right)=-\frac{1}{3}\).

Так как \(1\) не меняет число при умножении, то: \(1\cdot(-1)=-1\), \(1\cdot\frac{1}{3}=\frac{1}{3}\), \(1\cdot\left(-1\frac{1}{2}\right)=-1\frac{1}{2}\), \(1\cdot(-3)=-3\), \(1\cdot\left(-\frac{1}{2}\right)=-\frac{1}{2}\).

При умножении на \(-\frac{1}{2}\) знак меняется на противоположный, а модуль делится на \(2\): \(-\frac{1}{2}\cdot(-1)=\frac{1}{2}\), \(-\frac{1}{2}\cdot\frac{1}{3}=-\frac{1}{6}\), \(-\frac{1}{2}\cdot\left(-1\frac{1}{2}\right)=-\frac{1}{2}\cdot\left(-\frac{3}{2}\right)=\frac{3}{4}\), \(-\frac{1}{2}\cdot(-3)=\frac{3}{2}=1,5\), \(-\frac{1}{2}\cdot\left(-\frac{1}{2}\right)=\frac{1}{4}\).

Умножение на ноль всегда даёт ноль: \(0\cdot(-1)=0\), \(0\cdot\frac{1}{3}=0\), \(0\cdot\left(-1\frac{1}{2}\right)=0\), \(0\cdot(-3)=0\), \(0\cdot\left(-\frac{1}{2}\right)=0\).

При умножении на \(-2\) знак меняется, модуль умножается на \(2\); для смешанного числа \( -1\frac{1}{2}=-\frac{3}{2} \): \(-2\cdot(-1)=2\), \(-2\cdot\frac{1}{3}=-\frac{2}{3}\), \(-2\cdot\left(-1\frac{1}{2}\right)=-2\cdot\left(-\frac{3}{2}\right)=3\), \(-2\cdot(-3)=6\), \(-2\cdot\left(-\frac{1}{2}\right)=1\).

б) Деление заменяем умножением на обратное число: \(a:b=a\cdot\frac{1}{b}\) (при \(b\neq 0\)), знак определяем по правилам знаков. Тогда: \(\frac{1}{2}:2=\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}\), \(\frac{1}{2}:\left(-\frac{1}{2}\right)=\frac{1}{2}\cdot(-2)=-1\), \(\frac{1}{2}:(-6)=\frac{1}{2}\cdot\left(-\frac{1}{6}\right)=-\frac{1}{12}\), \(\frac{1}{2}:\frac{1}{6}=\frac{1}{2}\cdot 6=3\), \(\frac{1}{2}:\frac{1}{3}=\frac{1}{2}\cdot 3=\frac{3}{2}=1,5\).

Если делимое \(0\), то при любом ненулевом делителе частное \(0\): \(0:2=0\), \(0:\left(-\frac{1}{2}\right)=0\), \(0:(-6)=0\), \(0:\frac{1}{6}=0\), \(0:\frac{1}{3}=0\).

Для \(-1\): \(-1:2=-0,5\); \(-1:\left(-\frac{1}{2}\right)=-1\cdot(-2)=2\); \(-1:(-6)=\frac{1}{6}\); \(-1:\frac{1}{6}=-1\cdot 6=-6\); \(-1:\frac{1}{3}=-1\cdot 3=-3\).

Для \(-3\): \(-3:2=-1,5\); \(-3:\left(-\frac{1}{2}\right)=-3\cdot(-2)=6\); \(-3:(-6)=\frac{1}{2}=0,5\); \(-3:\frac{1}{6}=-3\cdot 6=-18\); \(-3:\frac{1}{3}=-3\cdot 3=-9\).

Для \(-\frac{2}{3}\): \(-\frac{2}{3}:2=-\frac{2}{3}\cdot\frac{1}{2}=-\frac{1}{3}\); \(-\frac{2}{3}:\left(-\frac{1}{2}\right)=-\frac{2}{3}\cdot(-2)=\frac{4}{3}=1\frac{1}{3}\); \(-\frac{2}{3}:(-6)=-\frac{2}{3}\cdot\left(-\frac{1}{6}\right)=\frac{1}{9}\); \(-\frac{2}{3}:\frac{1}{6}=-\frac{2}{3}\cdot 6=-4\); \(-\frac{2}{3}:\frac{1}{3}=-\frac{2}{3}\cdot 3=-2\).

а) При умножении рациональных чисел сначала определяем знак результата: если множители разных знаков, то произведение отрицательное, если одинаковых — положительное. Далее перемножаем модули: числители между собой и знаменатели между собой, а если есть смешанное число, то удобно перевести его в неправильную дробь. Например, \(-1\frac{1}{2}=-\frac{3}{2}\), поэтому \(\frac{2}{3}\cdot\left(-1\frac{1}{2}\right)=\frac{2}{3}\cdot\left(-\frac{3}{2}\right)\), после сокращения получается \(-1\).

\(\frac{2}{3}\cdot(-1)=-\frac{2}{3}\)
\(\frac{2}{3}\cdot\frac{1}{3}=\frac{2}{9}\)
\(\frac{2}{3}\cdot\left(-1\frac{1}{2}\right)=-\frac{2}{3}\cdot\frac{3}{2}=-1\)
\(\frac{2}{3}\cdot(-3)=-2\)
\(\frac{2}{3}\cdot\left(-\frac{1}{2}\right)=-\frac{1}{3}\)

Если множитель равен \(1\), то произведение равно второму множителю, потому что \(1\) — нейтральный элемент умножения: \(1\cdot a=a\). Поэтому здесь достаточно сохранить число во втором множителе, не меняя его знак и вид записи.

\(1\cdot(-1)=-1\)
\(1\cdot\frac{1}{3}=\frac{1}{3}\)
\(1\cdot\left(-1\frac{1}{2}\right)=-1\frac{1}{2}\)
\(1\cdot(-3)=-3\)
\(1\cdot\left(-\frac{1}{2}\right)=-\frac{1}{2}\)

При умножении на \(-\frac{1}{2}\) знак результата меняется на противоположный по сравнению со знаком второго множителя, потому что один множитель отрицательный. По модулю это «половина числа», то есть модуль результата равен \(\frac{1}{2}\) от модуля второго множителя; вычислительно это делается обычным умножением дробей. Например, \(\left(-\frac{1}{2}\right)\cdot\frac{1}{3}=-\frac{1}{6}\).

\(-\frac{1}{2}\cdot(-1)=\frac{1}{2}\)
\(-\frac{1}{2}\cdot\frac{1}{3}=-\frac{1}{6}\)
\(-\frac{1}{2}\cdot\left(-1\frac{1}{2}\right)=\frac{1}{2}\cdot\frac{3}{2}=\frac{3}{4}\)
\(-\frac{1}{2}\cdot(-3)=\frac{3}{2}=1,5\)
\(-\frac{1}{2}\cdot\left(-\frac{1}{2}\right)=\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}\)

При умножении на ноль всегда получаем ноль: \(0\cdot a=0\) для любого числа \(a\). Это следует из свойств умножения (ноль «обнуляет» произведение), поэтому здесь не нужны дополнительные преобразования — во всех случаях результат один и тот же.

\(0\cdot(-1)=0\)
\(0\cdot\frac{1}{3}=0\)
\(0\cdot\left(-1\frac{1}{2}\right)=0\)
\(0\cdot(-3)=0\)
\(0\cdot\left(-\frac{1}{2}\right)=0\)

При умножении на \(-2\) удобно помнить, что это удвоение модуля с изменением знака, так как множитель отрицательный. Если второй множитель отрицательный, то два «минуса» дают «плюс», и результат положительный. Смешанное число снова переводим в неправильную дробь: \(-1\frac{1}{2}=-\frac{3}{2}\), тогда \((-2)\cdot\left(-\frac{3}{2}\right)\) легко сокращается по \(2\).

\(-2\cdot(-1)=2\)
\(-2\cdot\frac{1}{3}=-\frac{2}{3}\)
\(-2\cdot\left(-1\frac{1}{2}\right)=2\cdot\frac{3}{2}=3\)
\(-2\cdot(-3)=6\)
\(-2\cdot\left(-\frac{1}{2}\right)=1\)

б) Деление на число удобно заменять умножением на обратное: \(a:b=a\cdot\frac{1}{b}\), если \(b\neq 0\). При делении дробей также следим за знаком: разные знаки дают отрицательный результат, одинаковые — положительный. Например, \(\frac{1}{2}:(-6)=\frac{1}{2}\cdot\left(-\frac{1}{6}\right)=-\frac{1}{12}\).

\(\frac{1}{2}:2=\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{4}\)
\(\frac{1}{2}:\left(-\frac{1}{2}\right)=\frac{1}{2}\cdot(-2)=-1\)
\(\frac{1}{2}:(-6)=\frac{1}{2}\cdot\left(-\frac{1}{6}\right)=-\frac{1}{12}\)
\(\frac{1}{2}:\frac{1}{6}=\frac{1}{2}\cdot 6=3\)
\(\frac{1}{2}:\frac{1}{3}=\frac{1}{2}\cdot 3=\frac{3}{2}=1,5\)

Если делимое равно нулю, то частное равно нулю при любом ненулевом делителе: \(0:b=0\) при \(b\neq 0\). Это потому, что \(0\) можно представить как \(0\cdot b\), и при обратной операции деления мы возвращаемся к нулю. Здесь все делители ненулевые, поэтому во всех случаях ответ \(0\).

\(0:2=0\)
\(0:\left(-\frac{1}{2}\right)=0\)
\(0:(-6)=0\)
\(0:\frac{1}{6}=0\)
\(0:\frac{1}{3}=0\)

При делении \(-1\) на положительное число результат отрицательный, а при делении на отрицательное — положительный. Деление на дробь заменяем умножением на обратную: \(-1:\frac{1}{6}=-1\cdot 6=-6\). Деление на \(-6\) даёт маленькую по модулю дробь, потому что делим единицу на большое число: \(-1:(-6)=\frac{1}{6}\).

\(-1:2=-0,5\)
\(-1:\left(-\frac{1}{2}\right)=1\cdot 2=2\)
\(-1:(-6)=\frac{1}{6}\)
\(-1:\frac{1}{6}=-1\cdot 6=-6\)
\(-1:\frac{1}{3}=-1\cdot 3=-3\)

В выражениях с \(-3\) используем те же правила: деление на \(2\) даёт \(-1,5\), потому что \(-3\) в \(2\) раза меньше по модулю, чем \(-6\). Деление на \(-\frac{1}{2}\) означает умножить на \(-2\), поэтому \(-3:\left(-\frac{1}{2}\right)=(-3)\cdot(-2)=6\). Деление на \(\frac{1}{6}\) и \(\frac{1}{3}\) превращается в умножение на \(6\) и на \(3\) соответственно, поэтому получаются \(-18\) и \(-9\).

\(-3:2=-1,5\)
\(-3:\left(-\frac{1}{2}\right)=3\cdot 2=6\)
\(-3:(-6)=3:6=0,5\)
\(-3:\frac{1}{6}=-3\cdot 6=-18\)
\(-3:\frac{1}{3}=-3\cdot 3=-9\)

Для \(-\frac{2}{3}\) деление на \(2\) — это умножение на \(\frac{1}{2}\): \(-\frac{2}{3}:2=-\frac{2}{3}\cdot\frac{1}{2}=-\frac{1}{3}\). Деление на \(-\frac{1}{2}\) заменяем умножением на \(-2\): \(-\frac{2}{3}:\left(-\frac{1}{2}\right)=-\frac{2}{3}\cdot(-2)=\frac{4}{3}=1\frac{1}{3}\). Деление на \(-6\) даёт положительную дробь \(\frac{1}{9}\), потому что делим отрицательное на отрицательное и одновременно уменьшаем модуль в \(6\) раз. Деление на \(\frac{1}{6}\) и \(\frac{1}{3}\) — это умножение на \(6\) и на \(3\), поэтому получаем \(-4\) и \(-2\).

\(-\frac{2}{3}:2=-\frac{1}{3}\)
\(-\frac{2}{3}:\left(-\frac{1}{2}\right)=\frac{2}{3}\cdot 2=\frac{4}{3}=1\frac{1}{3}\)
\(-\frac{2}{3}:(-6)=\frac{2}{3}\cdot\frac{1}{6}=\frac{1}{9}\)
\(-\frac{2}{3}:\frac{1}{6}=-\frac{2}{3}\cdot 6=-4\)
\(-\frac{2}{3}:\frac{1}{3}=-\frac{2}{3}\cdot 3=-2\)