ГДЗ по Математике 6 Класс Часть 2 Номер 36 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

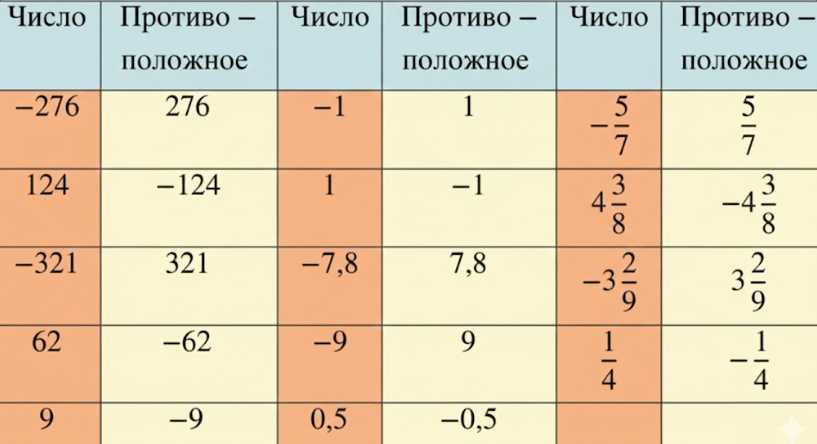
Найдите числа, противоположные числам: \(-276;\ 124;\ -321;\ 62;\ 9;\ -1;\ 1;\ -7,8;\ -9;\ 0,5;\ -\frac{5}{7};\ 4\frac{3}{8};\ -3\frac{2}{9};\ \frac{1}{4}\)

Противоположным числу называется число, отличающееся от данного только знаком. Для числа \(a\) противоположным является число \(-a\).

Понятие противоположного числа является фундаментальным в математике, особенно при изучении целых, рациональных и действительных чисел. Противоположное число для любого заданного числа \(a\) — это такое число \(-a\), которое при сложении с исходным числом \(a\) дает в результате нуль, то есть выполняется равенство \(a + (-a) = 0\). Геометрически, на числовой прямой, противоположные числа расположены на равном расстоянии от начала координат (нуля), но в противоположных направлениях. Например, число \(5\) находится на расстоянии \(5\) единиц в положительном направлении от нуля, а его противоположное число \(-5\) находится на расстоянии \(5\) единиц в отрицательном направлении от нуля. Таким образом, операция нахождения противоположного числа сводится к изменению знака исходного числа на противоположный.

Рассмотрим применение этого правила к различным типам чисел, представленным в таблице. Для целых чисел, таких как \(-276\), \(124\), \(-321\), \(62\), \(9\), \(-1\), \(1\), и \(-9\), нахождение противоположного числа происходит путем простой инверсии знака. Например, для \(-276\) противоположным будет \(276\), поскольку \(-276 + 276 = 0\). Для положительного числа \(124\) противоположным будет отрицательное число \(-124\). Аналогично, для \(-1\) противоположным является \(1\), а для \(9\) — \(-9\). Это правило едино для всех целых чисел: если число положительное, противоположное ему число отрицательное с тем же абсолютным значением, и наоборот.

При работе с десятичными и обыкновенными дробями, а также смешанными числами, принцип остается неизменным. Для десятичных дробей, таких как \(-7,8\) и \(0,5\), противоположные числа находятся как \(7,8\) и \(-0,5\) соответственно. Для обыкновенных дробей, например, \(-\frac{5}{7}\) и \(\frac{1}{4}\), противоположные числа будут \(\frac{5}{7}\) и \(-\frac{1}{4}\). В случае смешанных чисел, таких как \(4\frac{3}{8}\) и \(-3\frac{2}{9}\), знак меняется перед всем числом, включая целую и дробную части. Противоположным числу \(4\frac{3}{8}\) будет \(-4\frac{3}{8}\), а противоположным числу \(-3\frac{2}{9}\) будет \(3\frac{2}{9}\). Во всех случаях, сумма числа и его противоположного числа равна нулю, что подтверждает правильность нахождения противоположных значений.