ГДЗ по Математике 6 Класс Часть 2 Номер 355 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

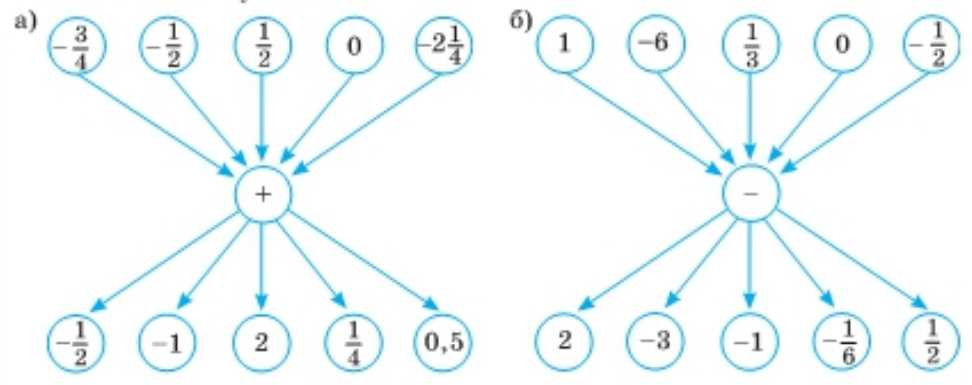
Вычислите устно:

а) Приводим дроби к общему знаменателю и складываем числители; десятичное \(0{,}5\) заменяем на \( \frac{1}{2}\), целые записываем как дроби при необходимости. Тогда получаем: \( -\frac{3}{4}+ \left(-\frac{1}{2}\right)=-\frac{5}{4}=-1\frac{1}{4}\), \( -\frac{3}{4}+(-1)=-1\frac{3}{4}\), \( -\frac{3}{4}+2=1\frac{1}{4}\), \( -\frac{3}{4}+\frac{1}{4}=-\frac{1}{2}\), \( -\frac{3}{4}+0{,}5=-\frac{1}{4}\).

Складываем аналогично для остальных строк, сводя к удобному виду: \( -\frac{1}{2}+ \left(-\frac{1}{2}\right)=-1\), \( -\frac{1}{2}+(-1)=-1\frac{1}{2}\), \( -\frac{1}{2}+2=1\frac{1}{2}\), \( -\frac{1}{2}+\frac{1}{4}=-\frac{1}{4}\), \( -\frac{1}{2}+0{,}5=0\).

Используем те же правила: \( \frac{1}{2}+ \left(-\frac{1}{2}\right)=0\), \( \frac{1}{2}+(-1)=-\frac{1}{2}\), \( \frac{1}{2}+2=2\frac{1}{2}\), \( \frac{1}{2}+\frac{1}{4}=\frac{3}{4}\), \( \frac{1}{2}+0{,}5=1\); \( 0+\left(-\frac{1}{2}\right)=-\frac{1}{2}\), \( 0+(-1)=-1\), \( 0+2=2\), \( 0+\frac{1}{4}=\frac{1}{4}\), \( 0+0{,}5=0{,}5\); \( -2\frac{1}{4}+\left(-\frac{1}{2}\right)=-2\frac{3}{4}\), \( -2\frac{1}{4}+(-1)=-3\frac{1}{4}\), \( -2\frac{1}{4}+2=-\frac{1}{4}\), \( -2\frac{1}{4}+\frac{1}{4}=-2\), \( -2\frac{1}{4}+0{,}5=-1\frac{3}{4}\).

б) Используем правило \(a-(-b)=a+b\); дроби приводим к общему знаменателю, десятичные при необходимости переводим в дроби. Тогда: \(1-2=-1\), \(1-(-3)=4\), \(1-(-1)=2\), \(1-\left(-\frac{1}{6}\right)=1\frac{1}{6}\), \(1-\frac{1}{2}=\frac{1}{2}\).

Дальше аналогично: \(-6-2=-8\), \(-6-(-3)=-3\), \(-6-(-1)=-5\), \(-6-\left(-\frac{1}{6}\right)=-5\frac{5}{6}\), \(-6-\frac{1}{2}=-6\frac{1}{2}\).

Приводим к знаменателю \(6\), где нужно: \( \frac{1}{3}-2=-1\frac{2}{3}\), \( \frac{1}{3}-(-3)=3\frac{1}{3}\), \( \frac{1}{3}-(-1)=1\frac{1}{3}\), \( \frac{1}{3}-\left(-\frac{1}{6}\right)=\frac{1}{2}\), \( \frac{1}{3}-\frac{1}{2}=-\frac{1}{6}\); \(0-2=-2\), \(0-(-3)=3\), \(0-(-1)=1\), \(0-\left(-\frac{1}{6}\right)=\frac{1}{6}\), \(0-\frac{1}{2}=-\frac{1}{2}\); \(-\frac{1}{2}-2=-2\frac{1}{2}\), \(-\frac{1}{2}-(-3)=2\frac{1}{2}\), \(-\frac{1}{2}-(-1)=\frac{1}{2}\), \(-\frac{1}{2}-\left(-\frac{1}{6}\right)=-\frac{1}{3}\), \(-\frac{1}{2}-\frac{1}{2}=-1\).

а) При сложении рациональных чисел удобно сначала привести дроби к общему знаменателю, чтобы корректно сложить (или вычесть) числители: например, \( -\frac{3}{4}+ \left(-\frac{1}{2}\right)\) переводим к знаменателю \(4\): \( -\frac{1}{2}=-\frac{2}{4}\), тогда \( -\frac{3}{4}+ \left(-\frac{2}{4}\right)=-\frac{5}{4}=-1\frac{1}{4}\). Если одно из слагаемых целое (например, \(2\) или \(-1\)), его удобно записывать в виде дроби с нужным знаменателем: \(2=\frac{8}{4}\), \(-1=-\frac{4}{4}\). Если встречается десятичное \(0{,}5\), переводим в обыкновенную дробь: \(0{,}5=\frac{1}{2}\), и дальше действуем так же, как с дробями.

\( -\frac{3}{4}+ \left(-\frac{1}{2}\right)=-\frac{3}{4}-\frac{2}{4}=-\frac{5}{4}=-1\frac{1}{4}\), \( -\frac{3}{4}+(-1)=-1\frac{3}{4}\), \( -\frac{3}{4}+2=1\frac{1}{4}\), \( -\frac{3}{4}+\frac{1}{4}=-\frac{2}{4}=-\frac{1}{2}\), \( -\frac{3}{4}+0{,}5=-\frac{3}{4}+\frac{1}{2}=-\frac{3}{4}+\frac{2}{4}=-\frac{1}{4}\). \( -\frac{1}{2}+ \left(-\frac{1}{2}\right)=-\frac{2}{2}=-1\), \( -\frac{1}{2}+(-1)=-1\frac{1}{2}\), \( -\frac{1}{2}+2=1\frac{1}{2}\), \( -\frac{1}{2}+\frac{1}{4}=-\frac{2}{4}+\frac{1}{4}=-\frac{1}{4}\), \( -\frac{1}{2}+0{,}5=-0{,}5+0{,}5=0\). \( \frac{1}{2}+ \left(-\frac{1}{2}\right)=0\), \( \frac{1}{2}+(-1)=-\frac{1}{2}\), \( \frac{1}{2}+2=2\frac{1}{2}\), \( \frac{1}{2}+\frac{1}{4}=\frac{2}{4}+\frac{1}{4}=\frac{3}{4}\), \( \frac{1}{2}+0{,}5=1\). \( 0+\left(-\frac{1}{2}\right)=-\frac{1}{2}\), \( 0+(-1)=-1\), \( 0+2=2\), \( 0+\frac{1}{4}=\frac{1}{4}\), \( 0+0{,}5=0{,}5\). \( -2\frac{1}{4}+\left(-\frac{1}{2}\right)=-\left(2\frac{1}{4}+\frac{1}{2}\right)=-\left(2\frac{1}{4}+\frac{2}{4}\right)=-2\frac{3}{4}\), \( -2\frac{1}{4}+(-1)=-3\frac{1}{4}\), \( -2\frac{1}{4}+2=-\frac{1}{4}\), \( -2\frac{1}{4}+\frac{1}{4}=-2\), \( -2\frac{1}{4}+0{,}5=-2\frac{1}{4}+\frac{1}{2}=-2\frac{1}{4}+\frac{2}{4}=-1\frac{3}{4}\).

б) При вычитании удобно помнить правило: \(a-(-b)=a+b\), то есть вычитание отрицательного числа заменяется сложением. Если вычитается дробь, работаем по тем же правилам, что и при сложении/вычитании дробей: приводим к общему знаменателю. Например, \(1-\left(-\frac{1}{6}\right)=1+\frac{1}{6}=1\frac{1}{6}\), а \( \frac{1}{3}-\frac{1}{2}\) считаем через общий знаменатель \(6\): \( \frac{1}{3}=\frac{2}{6}\), \( \frac{1}{2}=\frac{3}{6}\), значит \( \frac{2}{6}-\frac{3}{6}=-\frac{1}{6}\).

\(1-2=-1\), \(1-(-3)=4\), \(1-(-1)=2\), \(1-\left(-\frac{1}{6}\right)=1\frac{1}{6}\), \(1-\frac{1}{2}=\frac{1}{2}\). \(-6-2=-8\), \(-6-(-3)=-3\), \(-6-(-1)=-5\), \(-6-\left(-\frac{1}{6}\right)=-6+\frac{1}{6}=-5\frac{5}{6}\), \(-6-\frac{1}{2}=-6\frac{1}{2}\). \( \frac{1}{3}-2=-1\frac{2}{3}\), \( \frac{1}{3}-(-3)=3\frac{1}{3}\), \( \frac{1}{3}-(-1)=1\frac{1}{3}\), \( \frac{1}{3}-\left(-\frac{1}{6}\right)=\frac{2}{6}+\frac{1}{6}=\frac{3}{6}=\frac{1}{2}\), \( \frac{1}{3}-\frac{1}{2}=\frac{2}{6}-\frac{3}{6}=-\frac{1}{6}\). \(0-2=-2\), \(0-(-3)=3\), \(0-(-1)=1\), \(0-\left(-\frac{1}{6}\right)=\frac{1}{6}\), \(0-\frac{1}{2}=-\frac{1}{2}\). \(-\frac{1}{2}-2=-2\frac{1}{2}\), \(-\frac{1}{2}-(-3)=3-\frac{1}{2}=2\frac{1}{2}\), \(-\frac{1}{2}-(-1)=1-\frac{1}{2}=\frac{1}{2}\), \(-\frac{1}{2}-\left(-\frac{1}{6}\right)=-\frac{3}{6}+\frac{1}{6}=-\frac{2}{6}=-\frac{1}{3}\), \(-\frac{1}{2}-\frac{1}{2}=-1\).