ГДЗ по Математике 6 Класс Часть 2 Номер 300 Мнемозина Виленкин, Чесноков, Жохов, Шварцбурд — Подробные Ответы

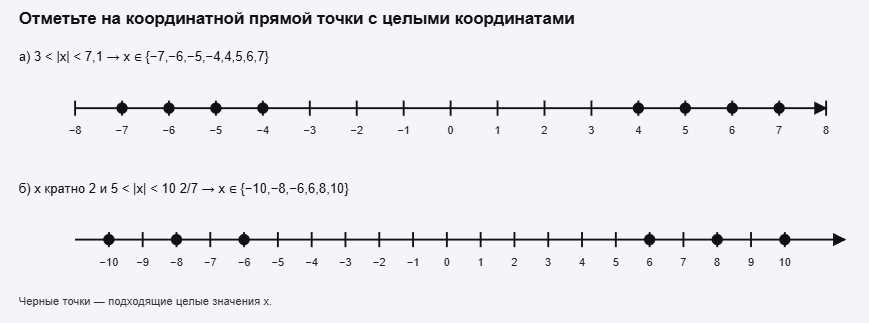
Отметьте на координатной прямой точки с целыми координатами:

а) модуль которых больше 3 и меньше 7,1;

б) кратными двум, модуль которых больше 5 и меньше \(10\frac{2}{7}\).

а) Условие \(3<|x|<7{,}1\), \(x\in\mathbb{Z}\). Так как \(x\) целое, то из \(3<|x|\) получаем \(|x|\ge 4\), а из \(|x|<7{,}1\) получаем \(|x|\le 7\). Ответ: \(-7;-6;-5;-4;4;5;6;7\).

б) Условие: \(x\) кратно \(2\), \(5<|x|<10\frac{2}{7}\), \(x\in\mathbb{Z}\). Так как \(10\frac{2}{7}<11\), то \(|x|\le 10\), а из \(5<|x|\) следует \(|x|\ge 6\); среди них берём чётные. Ответ: \(-10;-8;-6;6;8;10\).

а) Требуется отметить целые точки \(x\), для которых выполняется двойное неравенство \(3<|x|<7{,}1\). Модуль \(|x|\) — это расстояние от точки \(x\) до нуля на координатной прямой, поэтому условие \(3<|x|\) означает: точка должна находиться дальше, чем на 3 единицы от нуля, то есть \(x<-3\) или \(x>3\).

Далее учитываем условие \(|x|<7{,}1\): расстояние до нуля меньше \(7{,}1\), значит \(x\) находится между \(-7{,}1\) и \(7{,}1\), то есть \(-7{,}1<x<7{,}1\). Так как \(x\) должен быть целым, из \(-7{,}1<x<7{,}1\) получаем допустимые целые значения от \(-7\) до \(7\), а из условия «дальше, чем 3» исключаем \(-3,-2,-1,0,1,2,3\).

Итак, остаются целые числа, у которых \(|x|\) равен \(4,5,6\) или \(7\): \(-7;-6;-5;-4;4;5;6;7\). Именно эти точки нужно отметить на прямой: четыре слева от нуля и четыре симметрично справа.

б) Требуется найти целые \(x\), которые одновременно кратны двум и удовлетворяют \(5<|x|<10\frac{2}{7}\). Кратность двум означает, что \(x\) — чётное число, то есть \(x=2k\), где \(k\in\mathbb{Z}\), поэтому среди всех подходящих значений мы будем оставлять только чётные.

Условие \(5<|x|\) означает, что расстояние от \(x\) до нуля больше 5, следовательно, \(x<-5\) или \(x>5\). Условие \(|x|<10\frac{2}{7}\) ограничивает расстояние сверху: точка должна лежать ближе к нулю, чем \(10\frac{2}{7}\). Поскольку \(10\frac{2}{7}=10+\frac{2}{7}\) и это число больше 10, но меньше 11, то для целых \(x\) из \(|x|<10\frac{2}{7}\) следует \(|x|\le 10\).

Значит, по модулю возможны целые значения \(6,7,8,9,10\), но с учётом кратности двум остаются только \(|x|=6,8,10\). Тогда подходящие целые чётные числа: \(-10;-8;-6;6;8;10\), их и нужно отметить на координатной прямой.